The PT Symmeter

Miloslav Znojil

Non-Hermitian ring-shaped discrete lattices share the appeal with their more popular linear predecessors. Their dynamics controlled by the nearest-neighbor interaction is equally phenomenologically interesting. In comparison, the innovative nontriviality of their topology may be expected to lead to new spectral effects. Some of them are studied here via solvable examples. Main attention is paid to the perturbation-caused removals of spectral degeneracy at exceptional points.

http://arxiv.org/abs/1108.0620
Quantum Physics (quant-ph); Mathematical Physics (math-ph)

Miloslav Znojil

The one-dimensional real line of coordinates is replaced, for simplification or approximation purposes, by an N-plet of the so called Gauss-Hermite grid points. These grid points are interpreted as the eigenvalues of a tridiagonal matrix \(\mathfrak{q}_0\) which proves rather complicated. Via the “zeroth” Dyson-map \(\Omega_0\) the “operator of position” \(\mathfrak{q}_0\) is then further simplified into an isospectral matrix \(Q_0\) which is found optimal for the purpose. As long as the latter matrix appears non-Hermitian it is not an observable in the manifestly “false” Hilbert space \({\cal H}^{(F)}:=\mathbb{R}^N\). For this reason the optimal operator \(Q_0\) is assigned the family of its isospectral avatars \(\mathfrak{h}_\alpha\), \(\alpha=(0,)\,1,2,…\). They are, by construction, selfadjoint in the respective \(\alpha-\)dependent image Hilbert spaces \({\cal H}^{(P)}_\alpha\) obtained from \({\cal H}^{(F)}\) by the respective “new” Dyson maps \(\Omega_\alpha\). In the ultimate step of simplification, the inner product in the F-superscripted space is redefined in an {\it ad hoc}, $\alpha-$dependent manner. The resulting “simplest”, S-superscripted representations \({\cal H}^{(S)}_\alpha\) of the eligible physical Hilbert spaces of states (offering different dynamics) then emerge as, by construction, unitary equivalent to the (i.e., indistinguishable from the) respective awkward, P-superscripted and \(\alpha-\)subscripted physical Hilbert spaces.

http://arxiv.org/abs/1107.1770
Quantum Physics (quant-ph); Mathematical Physics (math-ph)

Miloslav Znojil

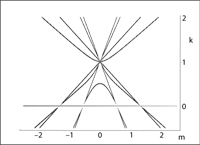A toy-model quantum system is proposed. At a given integer \(N\) it is defined by the pair of \(N\) by \(N\) real matrices \((H,\Theta)\) of which the first item \(H\) specifies an elementary, diagonalizable non-Hermitian Hamiltonian \(H \neq H^\dagger\) with the real and explicit spectrum given by the zeros of the \(N-\)th Chebyshev polynomial of the first kind. The second item \(\Theta\neq I\) must be (and is being) constructed as the related Hilbert-space metric which specifies the (in general, non-unique) physical inner product and which renders our toy-model Hamiltonian selfadjoint, i.e., compatible with the Dieudonne equation \(H^\dagger \Theta= \Theta\,H\). The elements of the (in principle, complete) set of the eligible metrics are then constructed in closed band-matrix form. They vary with our choice of the \(N-\)plet of optional parameters, \(\Theta=\Theta(\vec{\kappa})>0\) which must be (and are being) selected as lying in the positivity domain of the metric, \(\vec{\kappa} \in {\cal D}^{(physical)}\).

http://arxiv.org/abs/1105.1863
Quantum Physics (quant-ph); High Energy Physics – Lattice (hep-lat); Mathematical Physics (math-ph)

Miloslav Znojil

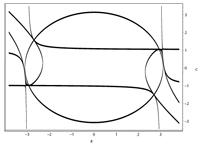The “Hermitizability” problem of quantum theory is explained, discussed and illustrated via the discrete-lattice cryptohermitian quantum graphs. In detail, the description of the domain ${\cal D}$ of admissible parameters is provided for the “circular-model” three-parametric quantum Hamiltonian $H$ using periodic boundary conditions. It is emphasized that even in such an elementary system the weak- and strong-coupling subdomains of ${\cal D}$ become, unexpectedly, non-empty and disconnected.

http://arxiv.org/abs/1103.4001
Quantum Physics (quant-ph); High Energy Physics – Theory (hep-th); Mathematical Physics (math-ph)

Miloslav Znojil

An array of N subsequent Laguerre polynomials is interpreted as an eigenvector of a non-Hermitian tridiagonal Hamiltonian $H$ with real spectrum or, better said, of an exactly solvable N-site-lattice cryptohermitian Hamiltonian whose spectrum is known as equal to the set of zeros of the N-th Laguerre polynomial. The two key problems (viz., the one of the ambiguity and the one of the closed-form construction of all of the eligible inner products which make $H$ Hermitian in the respective {\em ad hoc} Hilbert spaces) are discussed. Then, for illustration, the first four simplest, $k-$parametric definitions of inner products with $k=0,k=1,k=2$ and $k=3$ are explicitly displayed. In mathematical terms these alternative inner products may be perceived as alternative Hermitian conjugations of the initial N-plet of Laguerre polynomials. In physical terms the parameter $k$ may be interpreted as a measure of the “smearing of the lattice coordinates” in the model.

http://arxiv.org/abs/1101.1183
Mathematical Physics (math-ph); Quantum Physics (quant-ph)

Miloslav Znojil

Non-hermitian quantum graphs possessing real (i.e., in principle, observable) spectra are studied via their discretization. The discretized Hamiltonians are assigned, constructively, an elementary pseudometric and/or a more complicated metric. Both these constructions make the Hamiltonian Hermitian, respectively, in an auxiliary (Krein or Pontryagin) vector space or in a less friendly (but more useful) Hilbert space of quantum mechanics.

http://arxiv.org/abs/1101.1015
Quantum Physics (quant-ph); Mathematical Physics (math-ph)

Miloslav Znojil

In an innovative inverse-problem construction the measured, experimental energies $E_1$, $E_2$, …$E_N$ of a quantum bound-state system are assumed fitted by an N-plet of zeros of a classical orthogonal polynomial $f_N(E)$. We reconstruct the underlying Hamiltonian $H$ (in the most elementary nearest-neighbor-interaction form) and the underlying Hilbert space ${\cal H}$ of states (the rich menu of non-equivalent inner products is offered). The Gegenbauer’s ultraspherical polynomials $f_n(x)=C_n^\alpha(x)$ are chosen for the detailed illustration of technicalities.

http://arxiv.org/abs/1011.4803
Quantum Physics (quant-ph); Mathematical Physics (math-ph)
Phys. Rev. A 82 (2010) 052113
DOI:10.1103/PhysRevA.82.052113