Sergii Kuzhel, Oleksii Patsiuk
Let \(J\) and \(R\) be anti-commuting fundamental symmetries in a Hilbert space \(\mathfrak{H}\). The operators \(J\) and \(R\) can be interpreted as basis (generating) elements of the complex Clifford algebra \({\mathcal C}l_2(J,R):={span}\{I, J, R, iJR\}\). An arbitrary non-trivial fundamental symmetry from \({\mathcal C}l_2(J,R)\) is determined by the formula \(J_{\vec{\alpha}}=\alpha_{1}J+\alpha_{2}R+\alpha_{3}iJR\), where \({\vec{\alpha}}\in\mathbb{S}^2\). Let \(S\) be a symmetric operator that commutes with \({\mathcal C}l_2(J,R)\). The purpose of this paper is to study the sets \(\Sigma_{{J_{\vec{\alpha}}}}\) (\(\forall{\vec{\alpha}}\in\mathbb{S}^2)\) of self-adjoint extensions of \(S\) in Krein spaces generated by fundamental symmetries \({{J_{\vec{\alpha}}}}\) (\({{J_{\vec{\alpha}}}}\)-self-adjoint extensions). We show that the sets \(\Sigma_{{J_{\vec{\alpha}}}}\) and \(\Sigma_{{J_{\vec{\beta}}}}\) are unitarily equivalent for different \({\vec{\alpha}}, {\vec{\beta}}\in\mathbb{S}^2\) and describe in detail the structure of operators \(A\in\Sigma_{{J_{\vec{\alpha}}}}\) with empty resolvent set.
http://arxiv.org/abs/1105.2969
Functional Analysis (math.FA); Mathematical Physics (math-ph)
Jun-Qing Li, Yan-Gang Miao, Zhao Xue
An algebraic method for pseudo-hermitian systems is proposed through redefining annihilation and creation operators which are pseudo-hermitian adjoint to each other. As an example, a parity-pseudo-hermitian Hamiltonian is constructed and then analyzed in detail. Its real spectrum is obtained by means of the algebraic method, in which a new operator $V$ is introduced in order to define new annihilation and creation operators and to keep pseudo-hermitian inner products positive definite. It is shown that this P-pseudo-hermitian Hamiltonian also possesses PV-pseudo-hermiticity, where PV ensures a positive definite inner product. Moreover, when the parity-pseudo-hermitian system is extended to the canonical noncommutative space with noncommutative spatial coordinates and noncommutative momenta as well, the first order noncommutative correction of energy levels is calculated, and in particular the reality of energy spectra and the positive definiteness of inner products are found to be not altered by the noncommutativity.
http://arxiv.org/abs/1107.4972
Quantum Physics (quant-ph); High Energy Physics – Theory (hep-th)
S. Bittner, B. Dietz, U. Guenther, H. L. Harney, M. Miski-Oglu, A. Richter, F. Schaefer
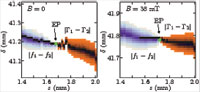We demonstrate the presence of parity-time (PT) symmetry for the non-Hermitian two-state Hamiltonian of a dissipative microwave billiard in the vicinity of an exceptional point (EP). The shape of the billiard depends on two parameters. The Hamiltonian is determined from the measured resonance spectrum on a fine grid in the parameter plane. On a curve, which passes through the EP, the Hamiltonian has either real or complex conjugate eigenvalues. An appropriate basis choice reveals its PT symmetry. Spontaneous symmetry breaking occurs at the EP.
http://arxiv.org/abs/1107.4256
Quantum Physics (quant-ph); Mathematical Physics (math-ph)
L. Jin, Z. Song
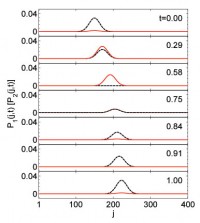We investigate the connection between pseudo-Hermitian and Hermitian descriptions for a lattice, which consists of a set of isomorphic pseudo-Hermitian clusters. We show that such non-Hermitian systems can act as Hermitian systems. This is made possible by considering the dynamics of a state involving the superposition of a single eigenmode of each isomorphic clusters. It still holds when multiple eigenmodes are involved when additional restriction on the state is imposed. This Hermitian dynamics is demonstrated for the case of an exactly solvable PT-symmetric ladder system.
http://arxiv.org/abs/1107.4311
Quantum Physics (quant-ph)
Carl M. Bender, Hugh F. Jones
All of the PT-symmetric potentials that have been studied so far have been local. In this paper nonlocal PT-symmetric separable potentials of the form \(V(x,y)=i\epsilon[U(x)U(y)-U(-x)U(-y)]\), where \(U(x)\) is real, are examined. Two specific models are examined. In each case it is shown that there is a parametric region of the coupling strength $\epsilon$ for which the PT symmetry of the Hamiltonian is unbroken and the bound-state energies are real. The critical values of \(\epsilon\) that bound this region are calculated.
http://arxiv.org/abs/1107.2293
High Energy Physics – Theory (hep-th); Mathematical Physics (math-ph); Quantum Physics (quant-ph)
Ali Mostafazadeh, Mustafa Sarisaman
The mathematical notion of a spectral singularity admits a physical interpretation as a zero-width resonance. It finds an optical realization as a certain type of lasing effect that occurs at the threshold gain. We explore spectral singularities of a complex spherical barrier potential and study their realization as transverse spherical electromagnetic waves emitted by a gain medium with a spherical geometry. In particular, for a typical dye laser material, we obtain a lower bound on the size of the gain medium for the occurence of this kind of spectral singularities.
http://arxiv.org/abs/1107.1873
Mathematical Physics (math-ph); Optics (physics.optics); Quantum Physics (quant-ph)
Miloslav Znojil
The one-dimensional real line of coordinates is replaced, for simplification or approximation purposes, by an N-plet of the so called Gauss-Hermite grid points. These grid points are interpreted as the eigenvalues of a tridiagonal matrix \(\mathfrak{q}_0\) which proves rather complicated. Via the “zeroth” Dyson-map \(\Omega_0\) the “operator of position” \(\mathfrak{q}_0\) is then further simplified into an isospectral matrix \(Q_0\) which is found optimal for the purpose. As long as the latter matrix appears non-Hermitian it is not an observable in the manifestly “false” Hilbert space \({\cal H}^{(F)}:=\mathbb{R}^N\). For this reason the optimal operator \(Q_0\) is assigned the family of its isospectral avatars \(\mathfrak{h}_\alpha\), \(\alpha=(0,)\,1,2,…\). They are, by construction, selfadjoint in the respective \(\alpha-\)dependent image Hilbert spaces \({\cal H}^{(P)}_\alpha\) obtained from \({\cal H}^{(F)}\) by the respective “new” Dyson maps \(\Omega_\alpha\). In the ultimate step of simplification, the inner product in the F-superscripted space is redefined in an {\it ad hoc}, $\alpha-$dependent manner. The resulting “simplest”, S-superscripted representations \({\cal H}^{(S)}_\alpha\) of the eligible physical Hilbert spaces of states (offering different dynamics) then emerge as, by construction, unitary equivalent to the (i.e., indistinguishable from the) respective awkward, P-superscripted and \(\alpha-\)subscripted physical Hilbert spaces.
http://arxiv.org/abs/1107.1770
Quantum Physics (quant-ph); Mathematical Physics (math-ph)
Ali Mostafazadeh
Using the Pais-Uhlenbeck Oscillator as a toy model, we outline a consistent alternative to the indefinite-metric quantization scheme that does not violate unitarity. We describe the basic mathematical structure of this method by giving an explicit construction of the Hilbert space of state vectors and the corresponding creation and annihilation operators. The latter satisfy the usual bosonic commutation relation and differ from those of the indefinite-metric theories by a sign in the definition of the creation operator. This change of sign achieves a definitization of the indefinite-metric that gives life to the ghost states without changing their contribution to the energy spectrum.
http://arxiv.org/abs/1107.1874
High Energy Physics – Theory (hep-th); General Relativity and Quantum Cosmology (gr-qc); Mathematical Physics (math-ph); Quantum Physics (quant-ph)
Kenta Esaki, Masatoshi Sato, Kazuki Hasebe, Mahito Kohmoto
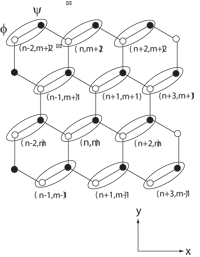Topological stability of the edge states is investigated for non-Hermitian systems. We examine two classes of non-Hermitian Hamiltonians supporting real bulk eigenenergies in weak non-Hermiticity: SU(1,1) and SO(3,2) Hamiltonians. As an SU(1,1) Hamiltonian, the tight-binding model on the honeycomb lattice with imaginary on-site potentials is examined. Edge states with ReE=0 and their topological stability are discussed by the winding number and the index theorem, based on the pseudo-anti-Hermiticity of the system. As a higher symmetric generalization of SU(1,1) Hamiltonians, we also consider SO(3,2) models. We investigate non-Hermitian generalization of the Luttinger Hamiltonian on the square lattice, and that of the Kane-Mele model on the honeycomb lattice, respectively. Using the generalized Kramers theorem for the time-reversal operator Theta with Theta^2=+1 [M. Sato et al., arXiv:1106.1806], we introduce a time-reversal invariant Chern number from which topological stability of gapless edge modes is argued.
http://arxiv.org/abs/1107.2079
Mesoscale and Nanoscale Physics (cond-mat.mes-hall); Other Condensed Matter (cond-mat.other)
Ali Mostafazadeh
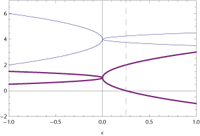We study the problem of locating spectral singularities of a general complex point interaction with a support at a single point. We also determine the bound states, examine the special cases where the point interaction is P-, T-, and PT-symmetric, and explore the issue of the coalescence of spectral singularities and bound states.
http://arxiv.org/abs/1107.1875
Mathematical Physics (math-ph); Quantum Physics (quant-ph)
