X. Q. Li, X. Z. Zhang, G. Zhang, Z. Song
We study the possibility of asymmetric transmission induced by a non-Hermitian scattering center embedded in a one-dimensional waveguide, motivated by the aim of realizing quantum diode in a non-Hermitian system. It is shown that a PT symmetric non-Hermitian scattering center always has symmetric transmission although the dynamics within the isolated center can be unidirectional, especially at its exceptional point. We propose a concrete scheme based on a flux-controlled non-Hermitian scattering center, which comprises a non-Hermitian triangular ring threaded by an Aharonov-Bohm flux. The analytical solution shows that such a complex scattering center acts as a diode at the resonant energy level of the spectral singularity, exhibiting perfect unidirectionality of the transmission. The connections between the phenomena of the asymmetric transmission and reflectionless absorption are also discussed.
http://arxiv.org/abs/1409.0420
Quantum Physics (quant-ph)
X. Z. Zhang, Z. Song
We study the geometric phase for the ground state of a generalized one-dimensional non-Hermitian quantum XY model, which has transverse-field-dependent intrinsic rotation-time reversal symmetry. Based on the exact solution, this model is shown to have full real spectrum in multiple regions for the finite size system. The result indicates that the phase diagram or exceptional boundary, which separates the unbroken and broken symmetry regions corresponds to the divergence of the Berry curvature. The scaling behaviors of the groundstate energy and Berry curvature are obtained in an analytical manner for a concrete system.
http://arxiv.org/abs/1308.4057
Quantum Physics (quant-ph)
X. Z. Zhang, Z. Song
We theoretically study the non-Hermitian systems, the non-Hermiticity of which arises from the unequal hopping amplitude (UHA) dimers. The distinguishing features of these models are that they have full real spectra if all of the eigenvectors are time-reversal (T) symmetric rather than parity-time-reversal (PT) symmetric, and that their Hermitian counterparts are shown to be an experimentally accessible system, which have the same topological structures as that of the original ones but modulated hopping amplitudes within the unbroken region. Under the reflectionless transmission condition, the scattering behavior of momentum-independent reflectionless transmission (RT) can be achieved in the concerned non-Hermitian system. This peculiar feature indicates that, for a certain class of non-Hermitian systems with a balanced combination of the RT dimers, the defects can appear fully invisible to an outside observer.
http://arxiv.org/abs/1306.1969
Quantum Physics (quant-ph)
X. Z. Zhang, L. Jin, Z. Song
Complex potential and non-Hermitian hopping amplitude are building blocks of a non-Hermitian quantum network. Appropriate configuration, such as PT-symmetric distribution, can lead to the full real spectrum. To investigate the underlying mechanism of this phenomenon, we study the phase diagram of a semi-infinite non-Hermitian system. It consists of a finite non-Hermitian cluster and a semi-infinite lead. Based on the analysis of the solution of the concrete systems, it is shown that it can have the full real spectrum without any requirements on the symmetry and the wave function within the lead becomes a unidirectional plane wave at the exceptional point. This universal dynamical behavior is demonstrated as the persistent emission and reflectionless absorption of wave packets in the typical non-Hermitian systems containing the complex on-site potential and non-Hermitian hopping amplitude.
http://arxiv.org/abs/1212.0086
Quantum Physics (quant-ph)
X. Z. Zhang, Z. Song
We systematically study the non-Hermitian version of the one-dimensional anisotropic XY model, which in its original form, is a unique exactly solvable quantum spin model for understanding the quantum phase transition. The distinguishing features of this model are that it has full real spectrum if all the eigenvectors are intrinsic rotation-time reversal (RT) symmetric rather than parity-time reversal (PT) symmetric, and that its Hermitian counterpart is shown approximately to be an experimentally accessible system, an isotropic XY spin chain with nearest neighbor coupling. Based on the exact solution, exceptional points which separated the unbroken and broken symmetry regions are obtained and lie on a hyperbola in the thermodynamic limit. It provides a nice paradigm to elucidate the complex quantum mechanics theory for a quantum spin system.
http://arxiv.org/abs/1210.5613
Quantum Physics (quant-ph)
L. Jin, Z. Song
We study the scattering problem for the non-Hermitian scattering center, which consists of two Hermitian clusters with anti-Hermitian couplings between them. Counterintuitively, it is shown that it acts as a Hermitian scattering center, satisfying \(|r| ^{2}+|t| ^{2}=1\), i.e., the Dirac probability current is conserved, when one of two clusters is embedded in the waveguides. This conclusion can be applied to an arbitrary parity-symmetric real Hermitian graph with additional PT-symmetric potentials, which is more feasible in experiment. Exactly solvable model is presented to illustrate the theory. Bethe ansatz solution indicates that the transmission spectrum of such a cluster displays peculiar feature arising from the non-Hermiticity of the scattering center.
http://arxiv.org/abs/1109.2187
Quantum Physics (quant-ph)
L. Jin, Z. Song
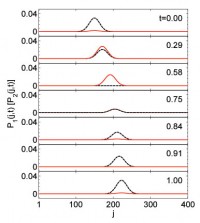 We investigate the connection between pseudo-Hermitian and Hermitian descriptions for a lattice, which consists of a set of isomorphic pseudo-Hermitian clusters. We show that such non-Hermitian systems can act as Hermitian systems. This is made possible by considering the dynamics of a state involving the superposition of a single eigenmode of each isomorphic clusters. It still holds when multiple eigenmodes are involved when additional restriction on the state is imposed. This Hermitian dynamics is demonstrated for the case of an exactly solvable PT-symmetric ladder system.
We investigate the connection between pseudo-Hermitian and Hermitian descriptions for a lattice, which consists of a set of isomorphic pseudo-Hermitian clusters. We show that such non-Hermitian systems can act as Hermitian systems. This is made possible by considering the dynamics of a state involving the superposition of a single eigenmode of each isomorphic clusters. It still holds when multiple eigenmodes are involved when additional restriction on the state is imposed. This Hermitian dynamics is demonstrated for the case of an exactly solvable PT-symmetric ladder system.
http://arxiv.org/abs/1107.4311
Quantum Physics (quant-ph)
X. Z. Zhang, L. Jin, Z. Song
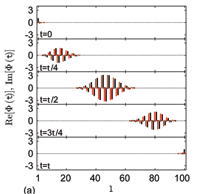 We systematically study the parity- and time-reversal- (PT) symmetric non-Hermitian version of a quantum network proposed in the work of Christandl et al. [Phys. Rev. Lett. 92, 187902 (2004)]. We show that such an extended model still allows conditional perfect state transfer within the unbroken PT-symmetric region, but not arbitrary. This is due to the fact that the evolution operator at certain period is equivalent to the PT operator for the real-valued wavefunction in the elaborate PT-symmetric Hilbert space. The critical behavior of the eigenstates is also discussed at the exceptional point.
We systematically study the parity- and time-reversal- (PT) symmetric non-Hermitian version of a quantum network proposed in the work of Christandl et al. [Phys. Rev. Lett. 92, 187902 (2004)]. We show that such an extended model still allows conditional perfect state transfer within the unbroken PT-symmetric region, but not arbitrary. This is due to the fact that the evolution operator at certain period is equivalent to the PT operator for the real-valued wavefunction in the elaborate PT-symmetric Hilbert space. The critical behavior of the eigenstates is also discussed at the exceptional point.
http://arxiv.org/abs/1106.0087
Quantum Physics (quant-ph)
L. Jin, Z. Song
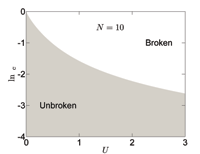 We study the phase diagram of a PT symmetric non-Hermitian Bose-Hubbard model. Using both analytical and numerical approaches, we find that even small on-site interaction can break the PT symmetry drastically. It has been demonstrated that the scaling law can be established for the exceptional point in small U limit. Based on numerical approach, we also find that the phase diagram shows rich structure for medium U: there exist multiple regions in which the PT symmetry is unbroken.
We study the phase diagram of a PT symmetric non-Hermitian Bose-Hubbard model. Using both analytical and numerical approaches, we find that even small on-site interaction can break the PT symmetry drastically. It has been demonstrated that the scaling law can be established for the exceptional point in small U limit. Based on numerical approach, we also find that the phase diagram shows rich structure for medium U: there exist multiple regions in which the PT symmetry is unbroken.
http://arxiv.org/abs/1105.6186
Statistical Mechanics (cond-mat.stat-mech); Quantum Physics (quant-ph)
L. Jin, Z. Song
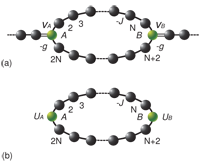 We explore a way of finding the link between a non-Hermitian Hamiltonian and a Hermitian one. Based on the analysis of Bethe Ansatz solutions for a class of non-Hermitian Hamiltonians and the scattering problems for the corresponding Hermitian Hamiltonians. It is shown that a scattering state of an arbitrary Hermitian lattice embedded in a chain as the scattering center shares the same wave function with the corresponding non-Hermitian tight binding lattice, which consists of the Hermitian lattice with two additional on-site complex potentials, no matter the non-Hermitian is broken PT symmetry or even non-PT. An exactly solvable model is presented to demonstrate the main points of this article.
We explore a way of finding the link between a non-Hermitian Hamiltonian and a Hermitian one. Based on the analysis of Bethe Ansatz solutions for a class of non-Hermitian Hamiltonians and the scattering problems for the corresponding Hermitian Hamiltonians. It is shown that a scattering state of an arbitrary Hermitian lattice embedded in a chain as the scattering center shares the same wave function with the corresponding non-Hermitian tight binding lattice, which consists of the Hermitian lattice with two additional on-site complex potentials, no matter the non-Hermitian is broken PT symmetry or even non-PT. An exactly solvable model is presented to demonstrate the main points of this article.
http://arxiv.org/abs/1101.0351
Quantum Physics (quant-ph)



