K. Li, P. G. Kevrekidis, B. A. Malomed
The subject of the work are pairs of linearly coupled PT-symmetric dimers. Two different settings are introduced, namely, straight-coupled dimers, where each gain site is linearly coupled to one gain and one loss site, and cross-coupled dimers, with each gain site coupled to two lossy ones. The latter pair with equal coupling coefficients represents a “PT-hypersymmetric” quadrimer. We find symmetric and antisymmetric solutions in these systems, chiefly in an analytical form, and explore the existence, stability and dynamical behavior of such solutions by means of numerical methods. We thus identify bifurcations occurring in the systems, including spontaneous symmetry breaking and saddle-center bifurcations. Simulations demonstrate that evolution of unstable branches typically leads to blowup. However, in some cases unstable modes rearrange into stable ones.
http://arxiv.org/abs/1312.3376
Pattern Formation and Solitons (nlin.PS); Optics (physics.optics)
K. Li, P. G. Kevrekidis, D. J. Frantzeskakis, C. E. Ruter, D. Kip
In this paper, we revisit one of the prototypical PT-symmetric oligomers, namely the trimer. We find all the relevant branches of “regular” solutions and analyze the bifurcations and instabilities thereof. Our work generalizes the formulation that was proposed recently in the case of dimers for the so-called “ghost states” of trimers, which we also identify and connect to symmetry-breaking bifurcations from the regular states. We also examine the dynamics of unstable trimers, as well as those of the ghost states in the parametric regime where the latter are found to exist. Finally, we present the current state of the art for optical experiments in PT-symmetric trimers, as well as experimental results in a gain-loss-gain three channel waveguide structure.
http://arxiv.org/abs/1306.2255
Quantum Physics (quant-ph)
K. Li, D. A. Zezyulin, V. V. Konotop, P. G. Kevrekidis
In this work, we propose a PT-symmetric coupler whose arms are birefringent waveguides as a realistic physical model which leads to a so-called quadrimer i.e., a four complex field setting. We seek stationary solutions of the resulting linear and nonlinear model, identifying its linear point of PT symmetry breaking and examining the corresponding nonlinear solutions that persist up to this point, as well as, so-called, ghost states that bifurcate from them. We obtain the relevant symmetry breaking bifurcations and numerically follow the associated dynamics which give rise to growth/decay even within the PT-symmetric phase. Our obtained stationary nonlinear solutions are found to terminate in saddle-center bifurcations which are analogous to the linear PT-phase transition.
http://arxiv.org/abs/1212.1676
Quantum Physics (quant-ph)
M. Duanmu, K. Li, R. L. Horne, P. G. Kevrekidis, N. Whitaker
In the present work we focus on the cases of two-site (dimer) and three-site (trimer) configurations, i.e. oligomers, respecting the parity-time (PT) symmetry, i.e., with a spatially odd gain-loss profile. We examine different types of solutions of such configurations with linear and nonlinear gain/loss profiles. Solutions beyond the linear PT-symmetry critical point as well as solutions with asymmetric linearization eigenvalues are found in both the nonlinear dimer and trimer. The latter feature is absent in linear PT-symmetric trimers, while both of them are absent in linear PT symmetric dimers. Furthermore, nonlinear gain/loss terms enable the existence of both symmetric and asymmetric solution profiles (and of bifurcations between them), while only symmetric solutions are present in the linear PT-symmetric dimers and trimers. The linear stability analysis around the obtained solutions is discussed and their dynamical evolution is explored by means of direct numerical simulations. Finally, a brief discussion is also given of recent progress in the context of PT-symmetric quadrimers.
http://arxiv.org/abs/1210.3871
Quantum Physics (quant-ph)
A.S. Rodrigues, K. Li, V. Achilleos, P.G. Kevrekidis, D.J. Frantzeskakis, Carl M. Bender
In this work we analyze PT-symmetric double-well potentials based on a two-mode picture. We reduce the problem into a PT-symmetric dimer and illustrate that the latter has effectively two fundamental bifurcations, a pitchfork (symmetry-breaking bifurcation) and a saddle-center one, which is the nonlinear analog of the PT-phase-transition. It is shown that the symmetry breaking leads to ghost states (amounting to growth or decay); although these states are not true solutions of the original continuum problem, the system’s dynamics closely follows them, at least in its metastable evolution. Past the second bifurcation, there are no longer states of the original continuum system. Nevertheless, the solutions can be analytically continued to yield a new pair of branches, which is also identified and dynamically examined. Our explicit analytical results for the dimer are directly compared to the full continuum problem, yielding a good agreement.
http://arxiv.org/abs/1207.1066
Pattern Formation and Solitons (nlin.PS); Quantum Gases (cond-mat.quant-gas); Mathematical Physics (math-ph)
K. Li, P.G. Kevrekidis
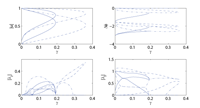 In the present work we focus on the case of (few-site) configurations respecting the PT-symmetry. We examine the case of such “oligomers” with not only 2-sites, as in earlier works, but also the cases of 3- and 4-sites. While in the former case of recent experimental interest, the picture of existing stationary solutions and their stability is fairly straightforward, the latter cases reveal a considerable additional complexity of solutions, including ones that exist past the linear PT-breaking point in the case of the trimer, and more complex, even asymmetric solutions in the case of the quadrimer with nontrivial spectral and dynamical properties. Both the linear stability and the nonlinear dynamical properties of the obtained solutions are discussed.
In the present work we focus on the case of (few-site) configurations respecting the PT-symmetry. We examine the case of such “oligomers” with not only 2-sites, as in earlier works, but also the cases of 3- and 4-sites. While in the former case of recent experimental interest, the picture of existing stationary solutions and their stability is fairly straightforward, the latter cases reveal a considerable additional complexity of solutions, including ones that exist past the linear PT-breaking point in the case of the trimer, and more complex, even asymmetric solutions in the case of the quadrimer with nontrivial spectral and dynamical properties. Both the linear stability and the nonlinear dynamical properties of the obtained solutions are discussed.
http://arxiv.org/abs/1102.0809
Pattern Formation and Solitons (nlin.PS); Quantum Gases (cond-mat.quant-gas)
