Andrea Cavaglia, Andreas Fring
We investigate for a large class of nonlinear wave equations, which allow for shock wave formations, how these solutions behave when they are PT-symmetrically deformed. For real solutions we find that they are transformed into peaked solutions with a discontinuity in the first derivative instead. The systems we investigate include the PT-symmetrically deformed inviscid Burgers equation recently studied by Bender and Feinberg, for which we show that it does not develop any shocks, but peaks instead. In this case we exploit the rare fact that the PT-deformation can be provided by an explicit map found by Curtright and Fairlie together with the property that the undeformed equation can be solved by the method of characteristics. We generalise the map and observe this type of behaviour for all integer values of the deformation parameter epsilon. The peaks are formed as a result of mapping the multi-valued self-avoiding shock profile to a multi-valued self-crossing function by means of the PT-deformation. For some deformation parameters we also investigate the deformation of complex solutions and demonstrate that in this case the deformation mechanism leads to discontinuties.
http://arxiv.org/abs/1201.5809
Mathematical Physics (math-ph); High Energy Physics – Theory (hep-th); Quantum Physics (quant-ph)
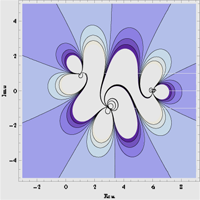We investigate complex versions of the Korteweg-deVries equations and an Ito type nonlinear system with two coupled nonlinear fields. We systematically construct rational, trigonometric/hyperbolic, elliptic and soliton solutions for these models and focus in particular on physically feasible systems, that is those with real energies. The reality of the energy is usually attributed to different realisations of an antilinear symmetry, as for instance PT-symmetry. It is shown that the symmetry can be spontaneously broken in two alternative ways either by specific choices of the domain or by manipulating the parameters in the solutions of the model, thus leading to complex energies. Surprisingly the reality of the energies can be regained in some cases by a further breaking of the symmetry on the level of the Hamiltonian. In many examples some of the fixed points in the complex solution for the field undergo a Hopf bifurcation in the PT-symmetry breaking process. By employing several different variants of the symmetries we propose many classes of new invariant extensions of these models and study their properties. The reduction of some of these models yields complex quantum mechanical models previously studied.