Li Ge, A. Douglas Stone
We consider the role of degeneracy in Parity-Time (PT) symmetry breaking for non-hermitian wave equations beyond one dimension. We show that if the spectrum is degenerate in the absence of T-breaking, and T is broken in a generic manner (without preserving other discrete symmetries), then the standard PT-symmetry breaking transition does not occur, meaning that the spectrum is complex even for infinitesimal strength of gain and loss. However the reality of the entire spectrum can be preserved over a finite interval if additional discrete symmetries X are imposed when T is broken, if X decouple all degenerate modes. When this is true only for a subset of the degenerate spectrum, there can be a partial PT transition in which this subset remains real over a finite interval of T-breaking. If the spectrum has odd-degeneracy, a fraction of the degenerate spectrum can remain in the symmetric phase even without imposing additional discrete symmetries, and they are analogous to dark states in atomic physics. These results are illustrated by the example of different T-breaking perturbations of a uniform dielectric disk and sphere. Finally, we show that multimode coupling is capable of restoring the PT-symmetric phase at finite T-breaking. We also analyze these questions when the parity operator is replaced by another spatial symmetry operator and find that the behavior can be qualitatively different.
http://arxiv.org/abs/1402.0428
Quantum Physics (quant-ph); Optics (physics.optics)
Philipp Ambichl, Konstantinos G. Makris, Li Ge, Yidong Chong, A. Douglas Stone, Stefan Rotter
PT-symmetric scattering systems with balanced gain and loss can undergo a symmetry-breaking transition in which the eigenvalues of the non-unitary scattering matrix change their phase shifts from real to complex values. We relate the PT-symmetry breaking points of such an unbounded scattering system to those of underlying bounded systems. In particular, we show how the PT-thresholds in the scattering matrix of the unbounded system translate into analogous transitions in the Robin boundary conditions of the corresponding bounded systems. Based on this relation, we argue and then confirm that the PT-transitions in the scattering matrix are, under very general conditions, entirely insensitive to a variable coupling strength between the bounded region and the unbounded asymptotic region, a result which can be tested experimentally.
http://arxiv.org/abs/1307.0149
Optics (physics.optics); Quantum Physics (quant-ph)
Y. D. Chong, Li Ge, A. Douglas Stone
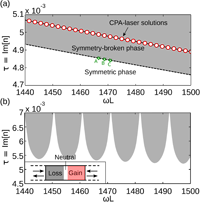 Using a scattering matrix formalism, we derive the general scattering properties of optical structures that are symmetric under a combination of parity and time-reversal (PT). We demonstrate the existence of a transition beween PT-symmetric scattering eigenstates, which are norm-preserving, and symmetry-broken pairs of eigenstates exhibiting net amplification and loss. The system proposed by Longhi, which can act simultaneously as a laser and coherent perfect absorber, occurs at discrete points in the broken symmetry phase, when a pole and zero of the S-matrix coincide.
Using a scattering matrix formalism, we derive the general scattering properties of optical structures that are symmetric under a combination of parity and time-reversal (PT). We demonstrate the existence of a transition beween PT-symmetric scattering eigenstates, which are norm-preserving, and symmetry-broken pairs of eigenstates exhibiting net amplification and loss. The system proposed by Longhi, which can act simultaneously as a laser and coherent perfect absorber, occurs at discrete points in the broken symmetry phase, when a pole and zero of the S-matrix coincide.
http://arxiv.org/abs/1008.5156
Optics (physics.optics); Quantum Physics (quant-ph)
