Yogesh N. Joglekar, Jacob L. Barnett
By investigating a parity and time-reversal (PT) symmetric, $N$-site lattice with impurities \(\pm i\gamma\) and hopping amplitudes \(t_0 (t_b)\) for regions outside (between) the impurity locations, we probe the origin of maximal PT-symmetry breaking that occurs when the impurities are nearest neighbors. Through a simple and exact derivation, we prove that the critical impurity strength is equal to the hopping amplitude between the impurities, \(\gamma_c=t_b\), and the simultaneous emergence of \(N\) complex eigenvalues is a robust feature of any PT-symmetric hopping profile. Our results show that the threshold strength \(\gamma_c\) can be widely tuned by a small change in the global profile of the lattice, and thus have experimental implications.
http://arxiv.org/abs/1108.6083
Quantum Physics (quant-ph); Statistical Mechanics (cond-mat.stat-mech)
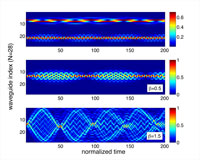Harsha Vemuri, Vaibhav Vavilala, Theja Bhamidipati, Yogesh N. Joglekar
Recently, waveguide lattices with non-uniform tunneling have been explored due to their myriad tunable properties, many of which arise from the extended nature of their eigenstates. Here, we investigate the dynamics, localization, and parity- and time-reversal-(PT) symmetry breaking in lattices with only localized eigenstates. We propose three families of tunneling profiles that lead to qualitatively different single-particle time evolution, and show that the effects of weak disorder contain signatures of the localized or extended nature of clean-lattice eigenstates. Our results suggest that waveguide lattices with only localized eigenstates will exhibit a wide array of phenomena that are absent in traditional systems.
http://arxiv.org/abs/1108.1402
Optics (physics.optics); Quantum Gases (cond-mat.quant-gas); Quantum Physics (quant-ph)
Derek D. Scott, Yogesh N. Joglekar
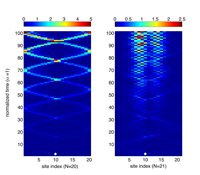We investigate the robustness of parity- and time-reversal PT-symmetric phase in an N-site lattice with position-dependent, parity-symmetric hopping function and a pair of imaginary, PT-symmetric impurities. We find that the “fragile” PT-symmetric phase in these lattices is stronger than its counterpart in a lattice with constant hopping. With an open system in mind, we explore the degrees of broken PT symmetry and their signatures in single-particle wavepacket evolution. We predict that when the PT-symmetric impurities are closest to each other, the time evolution of a wavepacket in an even-N lattice is remarkably different from that in an odd-$N$ lattice. Our results suggest that PT-symmetry breaking in such lattices is accompanied by rich, hitherto unanticipated, phenomena.
http://arxiv.org/abs/1104.1666
Quantum Physics (quant-ph); Quantum Gases (cond-mat.quant-gas)
Yogesh N. Joglekar, William A. Karr
We investigate the eigenvalue distribution $\sigma(x)$ and level-spacing distribution $p(s)$ of random matrices $M=AF\neq M^{\dagger}$ where $F$ is a diagonal inner-product and $A$ is a random, real symmetric or complex Hermitian matrix with independent entries drawn from a probability distribution $q(x)$ with zero mean and finite higher moments. Although not Hermitian, the matrix $M$ is self-adjoint with respect to $F$ and thus has a purely real spectrum. We find that the eigenvalue probability distribution $\sigma_F(x)$ is independent of the underlying distribution $q(x)$, is solely characterized by $F$, and therefore generalizes Wigner’s semicircle distribution $\sigma_W(x)$. We find that the level-spacing distributions $p(s)$ are independent of $q(x)$, are dependent upon the inner-product $F$ and whether $A$ is real or complex, and therefore generalize Wigner’s surmise for level spacing.
http://arxiv.org/abs/1012.1202
Disordered Systems and Neural Networks (cond-mat.dis-nn); Statistical Mechanics (cond-mat.stat-mech)