S. Ibáñez, S. Martí nez-Garaot, Xi Chen, E. Torrontegui, J. G. Muga
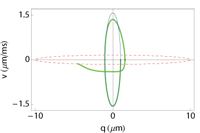Adiabatic processes driven by non-Hermitian, time-dependent Hamiltonians may be sped up by generalizing inverse engineering techniques based on Berry’s transitionless driving algorithm or on dynamical invariants. We work out the basic theory and examples described by two-level Hamiltonians: the acceleration of rapid adiabatic passage with a decaying excited level and of the dynamics of a classical particle on an expanding harmonic oscillator.
http://arxiv.org/abs/1106.2776
Quantum Physics (quant-ph)
Masatoshi Sato, Kazuki Hasebe, Kenta Esaki, Mahito Kohmoto
For ordinary hermitian Hamiltonians, the states show the Kramers degeneracy when the system has a half-odd-integer spin and the time reversal operator obeys \(\Theta^2=-1\), but no such a degeneracy exists when \(\Theta^2=+1\). Here we point out that for non-hermitian systems, there exists a degeneracy similar to Kramers even when \(\Theta^2=+1\). It is found that the new degeneracy follows from the mathematical structure of split-quaternion, instead of quaternion from which the Kramers degeneracy follows in the usual hermitian cases. Furthermore, we also show that particle/hole symmetry gives rise to a pair of states with opposite energies on the basis of the split quaternion in a class of non-hermitian Hamiltonians. As concrete examples, we examine in detail NxN Hamiltonians with N=2 and 4 which are non-hermitian generalizations of spin 1/2 Hamiltonian and quadrupole Hamiltonian of spin 3/2, respectively.
http://arxiv.org/abs/1106.1806
Statistical Mechanics (cond-mat.stat-mech); Mathematical Physics (math-ph); Quantum Physics (quant-ph)
Chao Zheng, Liang Hao, Gui Lu Long
Masillo [1] commented on our manuscript [2] “Observation of a Fast Evolution in a Parity-time-symmetric System”, pointing out a contradiction of our work with Ref.[3]. In this reply, we pointed out there is no disagreement between Masillo’s comment and our work in Ref. [2]. The efficiency cost pointed out in Ref.\cite{masillo} exists, namely to obtain the PT-symmetric hamiltonian evolution, one has to make a measurement on the auxiliary qubit and the auxiliary qubit is at state \(\left|0\right \rangle\) only probabilistically. This is reflected in the amplitude of the spectrum in the NMR quantum simulation. As a result, we made a small modification in a new version of the Ref. [2], and Fig. 2 of Ref.[2] has been replaced by spectra of two different \(\alpha\)’s in order to illustrate this fact.
http://arxiv.org/abs/1106.1848
Quantum Physics (quant-ph)
Fabio Masillo
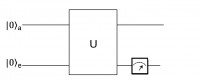In the paper “Observation of Fast Evolution in Parity-Time-Symmetric System” the authors propose a physical apparatus for the realization of a faster than Hermitian evolution. This last appears in contrast with the conclusions obtained in our paper “Some Remarks on Quantum Brachistochrone”. We will clarify this apparent contradiction and some problematic aspects of the treatment in [1].
http://arxiv.org/abs/1106.1550
Quantum Physics (quant-ph)
X. Z. Zhang, L. Jin, Z. Song
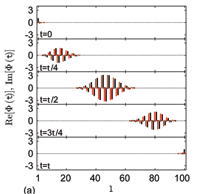We systematically study the parity- and time-reversal- (PT) symmetric non-Hermitian version of a quantum network proposed in the work of Christandl et al. [Phys. Rev. Lett. 92, 187902 (2004)]. We show that such an extended model still allows conditional perfect state transfer within the unbroken PT-symmetric region, but not arbitrary. This is due to the fact that the evolution operator at certain period is equivalent to the PT operator for the real-valued wavefunction in the elaborate PT-symmetric Hilbert space. The critical behavior of the eigenstates is also discussed at the exceptional point.
http://arxiv.org/abs/1106.0087
Quantum Physics (quant-ph)
Chao Zheng, Liang Hao, Gui Lu Long
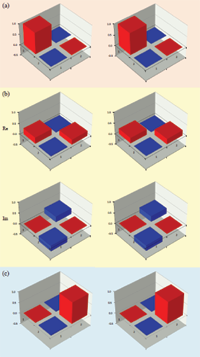To find and realize the optimal evolution between two states is significant both in theory and application. In quantum mechanics, the minimal evolution is bounded by the gap between the largest and smallest eigenvalue of the Hamiltonian. In the parity-time-symmetric(PT-symmetric) Hamiltonian theory, it was predicted that the optimized evolution time can be reduced drastically comparing to the bound in the Hermitian case, and can become even zero. In this Letter, we report the experimental observation of the fast evolution of a PT-symmetric Hamiltonian in an nuclear magnetic resonance (NMR) quantum system. The experimental results demonstrate that the PT-symmetric Hamiltonian can indeed evolve much faster than that in a quantum system, and time it takes can be arbitrary close to zero.
http://arxiv.org/abs/1105.6157
Quantum Physics (quant-ph)
L. Jin, Z. Song
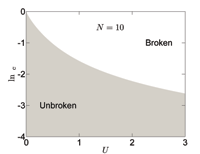We study the phase diagram of a PT symmetric non-Hermitian Bose-Hubbard model. Using both analytical and numerical approaches, we find that even small on-site interaction can break the PT symmetry drastically. It has been demonstrated that the scaling law can be established for the exceptional point in small U limit. Based on numerical approach, we also find that the phase diagram shows rich structure for medium U: there exist multiple regions in which the PT symmetry is unbroken.
http://arxiv.org/abs/1105.6186
Statistical Mechanics (cond-mat.stat-mech); Quantum Physics (quant-ph)
Wojciech Roga, Marek Smaczynski, Karol Zyczkowski
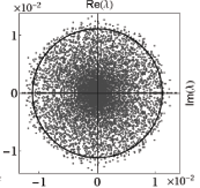Spectral properties of evolution operators corresponding to random maps and quantized chaotic systems strongly interacting with an environment can be described by the ensemble of non-hermitian random matrices from the real Ginibre ensemble. We analyze evolution operators \(\Psi=\Psi_s…\Psi_1\) representing the composition of s random maps and demonstrate that their complex eigenvalues are asymptotically described by the law of Burda et al. obtained for a product of s independent random complex Ginibre matrices. Numerical data support the conjecture that the same results are applicable to characterize the distribution of eigenvalues of the s-th power of a random Ginibre matrix. Squared singular values of Psi are shown to be described by the Fuss-Catalan distribution of order s. Results obtained for products of random Ginibre matrices are also capable to describe the s-step evolution operator for a model deterministic dynamical system – a generalized quantum baker map subjected to strong interaction with an environment.
http://arxiv.org/abs/1105.3830
Quantum Physics (quant-ph); Mathematical Physics (math-ph)
Johannes Sjoestrand
For a class of PT-symmetric operators with small random perturbations, the eigenvalues obey Weyl asymptotics with probability close to 1. Consequently, when the principal symbol is non-real, there are many non-real eigenvalues.
http://arxiv.org/abs/1105.4746
Spectral Theory (math.SP)
Dorje C. Brody, Eva-Maria Graefe
The dynamical aspects of a spin-1/2 particle in Hermitian coquaternionic quantum theory is investigated. It is shown that the time evolution exhibits three different characteristics, depending on the values of the parameters of the Hamiltonian. When energy eigenvalues are real, the evolution is either isomorphic to that of a complex Hermitian theory on a spherical state space, or else it remains unitary along an open orbit on a hyperbolic state space. When energy eigenvalues form a complex conjugate pair, the orbit of the time evolution closes again even though the state space is hyperbolic.
http://arxiv.org/abs/1105.4038
Mathematical Physics (math-ph); Quantum Physics (quant-ph)
