Wojciech Roga, Marek Smaczynski, Karol Zyczkowski
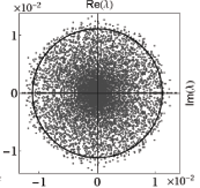 Spectral properties of evolution operators corresponding to random maps and quantized chaotic systems strongly interacting with an environment can be described by the ensemble of non-hermitian random matrices from the real Ginibre ensemble. We analyze evolution operators \(\Psi=\Psi_s…\Psi_1\) representing the composition of s random maps and demonstrate that their complex eigenvalues are asymptotically described by the law of Burda et al. obtained for a product of s independent random complex Ginibre matrices. Numerical data support the conjecture that the same results are applicable to characterize the distribution of eigenvalues of the s-th power of a random Ginibre matrix. Squared singular values of Psi are shown to be described by the Fuss-Catalan distribution of order s. Results obtained for products of random Ginibre matrices are also capable to describe the s-step evolution operator for a model deterministic dynamical system – a generalized quantum baker map subjected to strong interaction with an environment.
Spectral properties of evolution operators corresponding to random maps and quantized chaotic systems strongly interacting with an environment can be described by the ensemble of non-hermitian random matrices from the real Ginibre ensemble. We analyze evolution operators \(\Psi=\Psi_s…\Psi_1\) representing the composition of s random maps and demonstrate that their complex eigenvalues are asymptotically described by the law of Burda et al. obtained for a product of s independent random complex Ginibre matrices. Numerical data support the conjecture that the same results are applicable to characterize the distribution of eigenvalues of the s-th power of a random Ginibre matrix. Squared singular values of Psi are shown to be described by the Fuss-Catalan distribution of order s. Results obtained for products of random Ginibre matrices are also capable to describe the s-step evolution operator for a model deterministic dynamical system – a generalized quantum baker map subjected to strong interaction with an environment.
http://arxiv.org/abs/1105.3830
Quantum Physics (quant-ph); Mathematical Physics (math-ph)