Eva-Maria Graefe, Roman Schubert
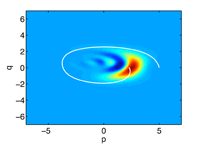 The quantum evolution of the Wigner function for Gaussian wave packets generated by a non-Hermitian Hamiltonian is investigated. In the semiclassical limit $\hbar\to 0$ this yields the non-Hermitian analog of the Ehrenfest theorem for the dynamics of observable expectation values. The lack of Hermiticity reveals the importance of the complex structure on the classical phase space: The resulting equations of motion are coupled to an equation of motion for the phase space metric—a phenomenon having no analogue in Hermitian theories. Furthermore, example studies show that the anti-Hermitian term can improve the accuracy of the classical approximation.
The quantum evolution of the Wigner function for Gaussian wave packets generated by a non-Hermitian Hamiltonian is investigated. In the semiclassical limit $\hbar\to 0$ this yields the non-Hermitian analog of the Ehrenfest theorem for the dynamics of observable expectation values. The lack of Hermiticity reveals the importance of the complex structure on the classical phase space: The resulting equations of motion are coupled to an equation of motion for the phase space metric—a phenomenon having no analogue in Hermitian theories. Furthermore, example studies show that the anti-Hermitian term can improve the accuracy of the classical approximation.
http://arxiv.org/abs/1010.4557
Quantum Physics (quant-ph); Mathematical Physics (math-ph)