Carl M. Bender, R. J. Kalveks
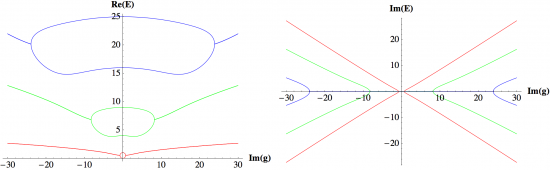
The E2 algebra has three elements, J, u, and v, which satisfy the commutation relations [u,J]=iv, [v,J]=-iu, [u,v]=0. We can construct the Hamiltonian H=J^2+gu, where g is a real parameter, from these elements. This Hamiltonian is Hermitian and consequently it has real eigenvalues. However, we can also construct the PT-symmetric and non-Hermitian Hamiltonian H=J^2+igu, where again g is real. As in the case of PT-symmetric Hamiltonians constructed from the elements x and p of the Heisenberg algebra, there are two regions in parameter space for this PT-symmetric Hamiltonian, a region of unbroken PT symmetry in which all the eigenvalues are real and a region of broken PT symmetry in which some of the eigenvalues are complex. The two regions are separated by a critical value of g.
http://arxiv.org/abs/1009.3236
High Energy Physics – Theory (hep-th); Mathematical Physics (math-ph); Quantum Physics (quant-ph)