Alois Regensburger, Mohammad-Ali Miri, Christoph Bersch, Jakob Näger, Georgy Onishchukov, Demetrios N. Christodoulides, Ulf Peschel
We provide the first experimental demonstration of defect states in parity-time (PT) symmetric mesh-periodic potentials. Our results indicate that these localized modes can undergo an abrupt phase transition in spite of the fact that they remain localized in a PT-symmetric periodic environment. Even more intriguing is the possibility of observing a linearly growing radiation emission from such defects provided their eigenvalue is associated with an exceptional point that resides within the continuum part of the spectrum. Localized complex modes existing outside the band-gap regions are also reported along with their evolution dynamics.
http://arxiv.org/abs/1301.1455
Optics (physics.optics); Quantum Physics (quant-ph)
Hamidreza Ramezani, D. N. Christodoulides, V. Kovanis, I. Vitebskiy, Tsampikos Kottos
We show that complex PT-symmetric photonic lattices can lead to a new class of self-imaging Talbot effects. For this to occur, we find that the input field pattern, has to respect specific periodicities which are dictated by the symmetries of the system. While at the spontaneous PT-symmetry breaking point, the image revivals occur at Talbot lengths governed by the characteristics of the passive lattice, at the exact phase it depends on the gain and loss parameter thus allowing one to control the imaging process.
http://arxiv.org/abs/1209.2349
Optics (physics.optics); Other Condensed Matter (cond-mat.other); Quantum Physics (quant-ph)
Mohammad-Ali Miri, Alejandro B. Aceves, Tsampikos Kottos, Vassilios Kovanis, Demetrios N. Christodoulides
It is shown that slow Bragg soliton solutions are possible in nonlinear complex parity-time (PT) symmetric periodic structures. Analysis indicates that the PT-symmetric component of the periodic optical refractive index can modify the grating band structure and hence the effective coupling between the forward and backward waves. Starting from a classical modified massive Thirring model, solitary wave solutions are obtained in closed form. The basic properties of these slow solitary waves and their dependence on their respective PT-symmetric gain/loss profile are then explored via numerical simulations.
http://arxiv.org/abs/1209.0787
Optics (physics.optics); Mathematical Physics (math-ph); Exactly Solvable and Integrable Systems (nlin.SI); Quantum Physics (quant-ph)
Alois Regensburger, Christoph Bersch, Mohammad-Ali Miri, Georgy Onishchukov, Demetrios N. Christodoulides, Ulf Peschel
The development of new artificial structures and materials is today one of the major research challenges in optics. In most studies so far, the design of such structures has been based on the judicious manipulation of their refractive index properties. Recently, the prospect of simultaneously using gain and loss was suggested as a new way of achieving optical behaviour that is at present unattainable with standard arrangements. What facilitated these quests is the recently developed notion of ‘parity–time symmetry’ in optical systems, which allows a controlled interplay between gain and loss. Here we report the experimental observation of light transport in large-scale temporal lattices that are parity–time symmetric. In addition, we demonstrate that periodic structures respecting this symmetry can act as unidirectional invisible media when operated near their exceptional points. Our experimental results represent a step in the application of concepts from parity–time symmetry to a new generation of multifunctional optical devices and networks.
http://dx.doi.org/10.1038/nature11298
Mohammad-Ali Miri, Alois Regensburger, Ulf Peschel, Demetrios N. Christodoulides
We investigate a new class of optical mesh periodic structures that are discretized in both the transverse and longitudinal directions. These networks are composed of waveguide arrays that are discretely coupled while phase elements are also inserted to discretely control their effective potentials and can be realized both in the temporal and the spatial domain. Their band structure and impulse response is studied in both the passive and parity-time (PT) symmetric regime. The possibility of band merging and the emergence of exceptional points along with the associated optical dynamics are considered in detail both above and below the PT-symmetry breaking point. Finally unidirectional invisibility in PT-synthetic mesh lattices is also examined along with possible superluminal light transport dynamics.
http://arxiv.org/abs/1208.1722
Quantum Physics (quant-ph)
Hamidreza Ramezani, Tsampikos Kottos, Vassilios Kovanis, Demetrios N. Christodoulides
We theoretically investigate the flow of electromagnetic waves in complex honeycomb photonic lattices with local PT symmetries. Such PT structure is introduced via a judicious arrangement of gain or loss across the honeycomb lattice, characterized by a gain/loss parameter \{\gamma\}. We found a new class of conical diffraction phenomena where the formed cone is brighter and travels along the lattice with a transverse speed proportional to \{\sqrt{\gamma}\}.
http://arxiv.org/abs/1112.4734
Optics (physics.optics); Quantum Physics
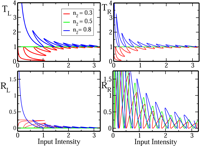 Zin Lin, Hamidreza Ramezani, Toni Eichelkraut, Tsampikos Kottos, Hui Cao, Demetrios N. Christodoulides
Zin Lin, Hamidreza Ramezani, Toni Eichelkraut, Tsampikos Kottos, Hui Cao, Demetrios N. Christodoulides
We show that parity-time (PT) symmetric Bragg periodic structures, near the spontaneous PT – symmetry breaking point, can act as unidirectional invisible media. In this regime, the re flection from one end is diminished while it is enhanced from the other. At the same time the transmission coefficient and phase, are indistinguishable from those expected in the absence of a grating. The phenomenon is robust even in the presence of Kerr non-linearities, and it can also eff?ectively suppress optical bistabilities.
http://arxiv.org/abs/1108.2493
Optics (physics.optics)
