D. Dutta, O. Panella, P. Roy
We study generalized Dirac oscillators with complex interactions in \((1+1)\) dimensions. It is shown that for the choice of interactions considered here, the Dirac Hamiltonians are \(\eta\) pseudo Hermitian with respect to certain metric operators \(\eta\). Exact solutions of the generalized Dirac Oscillator for some choices of the interactions have also been obtained. It is also shown that generalized Dirac oscillators can be identified with Anti Jaynes Cummings type model and by spin flip it can also be identified with Jaynes Cummings type model.
http://arxiv.org/abs/1301.2035
Mathematical Physics (math-ph); High Energy Physics – Theory (hep-th); Quantum Physics (quant-ph)
David Gomez-Ullate, Paolo Santini, Matteo Sommacal, Francesco Calogero
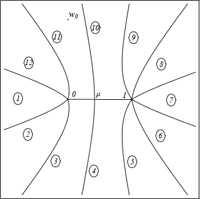 We provide an example of how the complex dynamics of a recently introduced model can be understood via a detailed analysis of its associated Riemann surface. Thanks to this geometric description an explicit formula for the period of the orbits can be derived, which is shown to depend on the initial data and the continued fraction expansion of a simple ratio of the coupling constants of the problem. For rational values of this ratio and generic values of the initial data, all orbits are periodic and the system is isochronous. For irrational values of the ratio, there exist periodic and quasi-periodic orbits for different initial data. Moreover, the dependence of the period on the initial data shows a rich behavior and initial data can always be found such the period is arbitrarily high.
We provide an example of how the complex dynamics of a recently introduced model can be understood via a detailed analysis of its associated Riemann surface. Thanks to this geometric description an explicit formula for the period of the orbits can be derived, which is shown to depend on the initial data and the continued fraction expansion of a simple ratio of the coupling constants of the problem. For rational values of this ratio and generic values of the initial data, all orbits are periodic and the system is isochronous. For irrational values of the ratio, there exist periodic and quasi-periodic orbits for different initial data. Moreover, the dependence of the period on the initial data shows a rich behavior and initial data can always be found such the period is arbitrarily high.
http://arxiv.org/abs/1104.2205
Chaotic Dynamics (nlin.CD); Dynamical Systems (math.DS); Exactly Solvable and Integrable Systems (nlin.SI)
