Jia-wen Deng, Uwe Guenther, Qing-hai Wang
Three ways of constructing a non-Hermitian matrix with possible all real eigenvalues are discussed. They are PT symmetry, pseudo-Hermiticity, and generalized PT symmetry. Parameter counting is provided for each class. All three classes of matrices have more real parameters than a Hermitian matrix with the same dimension. The generalized PT-symmetric matrices are most general among the three. All self-adjoint matrices process a generalized PT symmetry. For a given matrix, it can be both PT-symmetric and P’-pseudo-Hermitian with respect to some P’ operators. The relation between corresponding P and P’ operators is established. The Jordan block structures of each class are discussed. Explicit examples in 2×2 are shown.
http://arxiv.org/abs/1212.1861
Quantum Physics (quant-ph); Mathematical Physics (math-ph)
Raam Uzdin, Uwe Guenther, Saar Rahav, Nimrod Moiseyev
The evolution speed in projective Hilbert space is considered for Hermitian Hamiltonians and for non-Hermitian (NH) ones. Based on the Hilbert-Schmidt norm and the spectral norm of a Hamiltonian, resource-related upper bounds on the evolution speed are constructed. These bounds are valid also for NH Hamiltonians and they are illustrated for an optical NH Hamiltonian and for a non-Hermitian \(\mathcal{PT}\)-symmetric matrix Hamiltonian. Furthermore, the concept of quantum speed efficiency is introduced as measure of the system resources directly spent on the motion in the projective Hilbert space. A recipe for the construction of time-dependent Hamiltonians which ensure 100% speed efficiency is given. Generally these efficient Hamiltonians are NH but there is a Hermitian efficient Hamiltonian as well. Finally, the extremal case of a non-Hermitian non-diagonalizable Hamiltonian with vanishing energy difference is shown to produce a 100% efficient evolution with minimal resources consumption.
http://arxiv.org/abs/1207.5373
Quantum Physics (quant-ph)
Hamidreza Ramezani, J. Schindler, F. M. Ellis, Uwe Guenther, Tsampikos Kottos
The beat time \({\tau}_{fpt}\) associated with the energy transfer between two coupled oscillators is dictated by the bandwidth theorem which sets a lower bound \({\tau}_{fpt}\sim 1/{\delta}{\omega}\). We show, both experimentally and theoretically, that two coupled active LRC electrical oscillators with parity-time (PT) symmetry, bypass the lower bound imposed by the bandwidth theorem, reducing the beat time to zero while retaining a real valued spectrum and fixed eigenfrequency difference \(\delta\omega\). Our results foster new design strategies which lead to (stable) pseudo-unitary wave evolution, and may allow for ultrafast computation, telecommunication, and signal processing.
http://arxiv.org/abs/1205.1847
Classical Physics (physics.class-ph)
Kai Li, P. G. Kevrekidis, Boris A. Malomed, Uwe Guenther
We introduce four basic two-dimensional (2D) plaquette configurations with onsite cubic nonlinearities, which may be used as building blocks for 2D PT -symmetric lattices. For each configuration, we develop a dynamical model and examine its PT symmetry. The corresponding nonlinear modes are analyzed starting from the Hamiltonian limit, with zero value of the gain-loss coefficient. Once the relevant waveforms have been identified (chiefly, in an analytical form), their stability is examined by means of linearization in the vicinity of stationary points. This reveals diverse and, occasionally, fairly complex bifurcations. The evolution of unstable modes is explored by means of direct simulations. In particular, stable localized modes are found in these systems, although the majority of identified solutions is unstable.
http://arxiv.org/abs/1204.5530
Quantum Physics (quant-ph); High Energy Physics – Theory (hep-th)
Oleg N. Kirillov
When gain and loss are in perfect balance, dynamical systems with indefinite damping can obey the exact PT-symmetry and therefore be marginally stable with a pure imaginary spectrum. At an exceptional point where the exact PT-symmetry is spontaneously broken, the stability is lost via a Krein collision of eigenvalues just as it happens at the Hamiltonian Hopf bifurcation. In the parameter space of a general dissipative system, marginally stable PT-symmetric ones occupy singularities on the boundary of the asymptotic stability domain. To observe how the singular surface governs dissipation-induced destabilization of the PT-symmetric system when gain and loss are not matched, an extension of recent experiments with PT-symmetric LRC circuits is proposed.
http://arxiv.org/abs/1110.0018
Mathematical Physics (math-ph); Other Condensed Matter (cond-mat.other); Spectral Theory (math.SP); Quantum Physics (quant-ph)
S. Bittner, B. Dietz, U. Guenther, H. L. Harney, M. Miski-Oglu, A. Richter, F. Schaefer
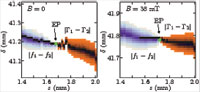 We demonstrate the presence of parity-time (PT) symmetry for the non-Hermitian two-state Hamiltonian of a dissipative microwave billiard in the vicinity of an exceptional point (EP). The shape of the billiard depends on two parameters. The Hamiltonian is determined from the measured resonance spectrum on a fine grid in the parameter plane. On a curve, which passes through the EP, the Hamiltonian has either real or complex conjugate eigenvalues. An appropriate basis choice reveals its PT symmetry. Spontaneous symmetry breaking occurs at the EP.
We demonstrate the presence of parity-time (PT) symmetry for the non-Hermitian two-state Hamiltonian of a dissipative microwave billiard in the vicinity of an exceptional point (EP). The shape of the billiard depends on two parameters. The Hamiltonian is determined from the measured resonance spectrum on a fine grid in the parameter plane. On a curve, which passes through the EP, the Hamiltonian has either real or complex conjugate eigenvalues. An appropriate basis choice reveals its PT symmetry. Spontaneous symmetry breaking occurs at the EP.
http://arxiv.org/abs/1107.4256
Quantum Physics (quant-ph); Mathematical Physics (math-ph)
