Kazunari Hashimoto, Kazuki Kanki, Hisao Hayakawa, Tomio Petrosky
We propose a regular representation for a non-Hermitian operator even if the parameter space contains exceptional points (EPs), at which the operator cannot be diagonalized and the usual spectral representation ceases to exist. Our representation has a generalized Jordan block form and is written in terms of extended pseudo-eigenstates. Our method is free from the difficulty of the singularity of the spectral representation at EPs, at which multiple eigenvalues and eigenvectors coalesce and the eigenvectors cannot be normalized. Our representation improves the accuracy of numerical calculations of physical quantities near EPs. We also find that our method is applicable to various problems related to EPs in the parameter space of non-Hermitian operators. We demonstrate the usefulness of our representation by investigating Boltzmann’s collision operator in a one-dimensional quantum Lorentz gas in the weak coupling approximation.
http://arxiv.org/abs/1409.7453
Statistical Mechanics (cond-mat.stat-mech)
Carl M. Bender, Mariagiovanna Gianfreda
In 1980 Englert examined the classic problem of the electromagnetic self-force on an oscillating charged particle. His approach, which was based on an earlier idea of Bateman, was to introduce a charge-conjugate particle and to show that the two-particle system is Hamiltonian. Unfortunately, Englert’s model did not solve the problem of runaway modes, and the corresponding quantum theory had ghost states. It is shown here that Englert’s Hamiltonian is PT symmetric, and that the problems with his model arise because the PT symmetry is broken at both the classical and quantum level. However, by allowing the charged particles to interact and by adjusting the coupling parameters to put the model into an unbroken PT-symmetric region, one eliminates the classical runaway modes and obtains a corresponding quantum system that is ghost free.
http://arxiv.org/abs/1409.3828
High Energy Physics – Theory (hep-th); Mathematical Physics (math-ph); Quantum Physics (quant-ph)
Naomichi Hatano
Two theoretical methods of finding resonant states in open quantum systems, namely the approach of the Siegert boundary condition and the Feshbach formalism, are reviewed and shown to be algebraically equivalent to each other for a simple model of the T-type quantum dot. It is stressed that the seemingly Hermitian Hamiltonian of an open quantum system is implicitly non-Hermitian outside the Hilbert space. The two theoretical approaches extract an explicitly non-Hermitian effective Hamiltonian in a contracted space out of the seemingly Hermitian (but implicitly non-Hermitian) full Hamiltonian in the infinite-dimensional state space of an open quantum system.
http://arxiv.org/abs/1405.7021
Quantum Physics (quant-ph); Mesoscale and Nanoscale Physics (cond-mat.mes-hall); Mathematical Physics (math-ph); Nuclear Theory (nucl-th)
Kenta Esaki, Masatoshi Sato, Kazuki Hasebe, Mahito Kohmoto
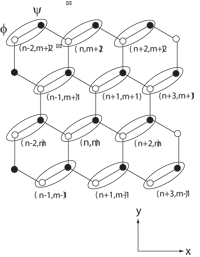 Topological stability of the edge states is investigated for non-Hermitian systems. We examine two classes of non-Hermitian Hamiltonians supporting real bulk eigenenergies in weak non-Hermiticity: SU(1,1) and SO(3,2) Hamiltonians. As an SU(1,1) Hamiltonian, the tight-binding model on the honeycomb lattice with imaginary on-site potentials is examined. Edge states with ReE=0 and their topological stability are discussed by the winding number and the index theorem, based on the pseudo-anti-Hermiticity of the system. As a higher symmetric generalization of SU(1,1) Hamiltonians, we also consider SO(3,2) models. We investigate non-Hermitian generalization of the Luttinger Hamiltonian on the square lattice, and that of the Kane-Mele model on the honeycomb lattice, respectively. Using the generalized Kramers theorem for the time-reversal operator Theta with Theta^2=+1 [M. Sato et al., arXiv:1106.1806], we introduce a time-reversal invariant Chern number from which topological stability of gapless edge modes is argued.
Topological stability of the edge states is investigated for non-Hermitian systems. We examine two classes of non-Hermitian Hamiltonians supporting real bulk eigenenergies in weak non-Hermiticity: SU(1,1) and SO(3,2) Hamiltonians. As an SU(1,1) Hamiltonian, the tight-binding model on the honeycomb lattice with imaginary on-site potentials is examined. Edge states with ReE=0 and their topological stability are discussed by the winding number and the index theorem, based on the pseudo-anti-Hermiticity of the system. As a higher symmetric generalization of SU(1,1) Hamiltonians, we also consider SO(3,2) models. We investigate non-Hermitian generalization of the Luttinger Hamiltonian on the square lattice, and that of the Kane-Mele model on the honeycomb lattice, respectively. Using the generalized Kramers theorem for the time-reversal operator Theta with Theta^2=+1 [M. Sato et al., arXiv:1106.1806], we introduce a time-reversal invariant Chern number from which topological stability of gapless edge modes is argued.
http://arxiv.org/abs/1107.2079
Mesoscale and Nanoscale Physics (cond-mat.mes-hall); Other Condensed Matter (cond-mat.other)
Masatoshi Sato, Kazuki Hasebe, Kenta Esaki, Mahito Kohmoto
For ordinary hermitian Hamiltonians, the states show the Kramers degeneracy when the system has a half-odd-integer spin and the time reversal operator obeys \(\Theta^2=-1\), but no such a degeneracy exists when \(\Theta^2=+1\). Here we point out that for non-hermitian systems, there exists a degeneracy similar to Kramers even when \(\Theta^2=+1\). It is found that the new degeneracy follows from the mathematical structure of split-quaternion, instead of quaternion from which the Kramers degeneracy follows in the usual hermitian cases. Furthermore, we also show that particle/hole symmetry gives rise to a pair of states with opposite energies on the basis of the split quaternion in a class of non-hermitian Hamiltonians. As concrete examples, we examine in detail NxN Hamiltonians with N=2 and 4 which are non-hermitian generalizations of spin 1/2 Hamiltonian and quadrupole Hamiltonian of spin 3/2, respectively.
http://arxiv.org/abs/1106.1806
Statistical Mechanics (cond-mat.stat-mech); Mathematical Physics (math-ph); Quantum Physics (quant-ph)
