L. Jin, Z. Song
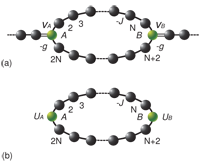
We investigate the connection between pseudo-Hermitian and Hermitian descriptions for a lattice, which consists of a set of isomorphic pseudo-Hermitian clusters. We show that such non-Hermitian systems can act as Hermitian systems. This is made possible by considering the dynamics of a state involving the superposition of a single eigenmode of each isomorphic clusters. It still holds when multiple eigenmodes are involved when additional restriction on the state is imposed. This Hermitian dynamics is demonstrated for the case of an exactly solvable PT-symmetric ladder system.
http://arxiv.org/abs/1107.4311
Quantum Physics (quant-ph)
X. Z. Zhang, L. Jin, Z. Song
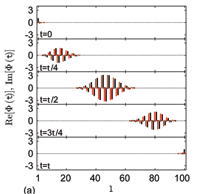We systematically study the parity- and time-reversal- (PT) symmetric non-Hermitian version of a quantum network proposed in the work of Christandl et al. [Phys. Rev. Lett. 92, 187902 (2004)]. We show that such an extended model still allows conditional perfect state transfer within the unbroken PT-symmetric region, but not arbitrary. This is due to the fact that the evolution operator at certain period is equivalent to the PT operator for the real-valued wavefunction in the elaborate PT-symmetric Hilbert space. The critical behavior of the eigenstates is also discussed at the exceptional point.
http://arxiv.org/abs/1106.0087
Quantum Physics (quant-ph)
L. Jin, Z. Song
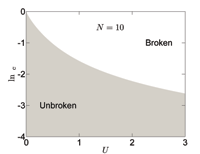We study the phase diagram of a PT symmetric non-Hermitian Bose-Hubbard model. Using both analytical and numerical approaches, we find that even small on-site interaction can break the PT symmetry drastically. It has been demonstrated that the scaling law can be established for the exceptional point in small U limit. Based on numerical approach, we also find that the phase diagram shows rich structure for medium U: there exist multiple regions in which the PT symmetry is unbroken.
http://arxiv.org/abs/1105.6186
Statistical Mechanics (cond-mat.stat-mech); Quantum Physics (quant-ph)
L. Jin, Z. Song
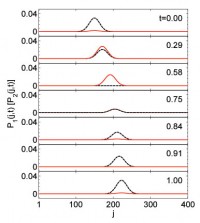
We explore a way of finding the link between a non-Hermitian Hamiltonian and a Hermitian one. Based on the analysis of Bethe Ansatz solutions for a class of non-Hermitian Hamiltonians and the scattering problems for the corresponding Hermitian Hamiltonians. It is shown that a scattering state of an arbitrary Hermitian lattice embedded in a chain as the scattering center shares the same wave function with the corresponding non-Hermitian tight binding lattice, which consists of the Hermitian lattice with two additional on-site complex potentials, no matter the non-Hermitian is broken PT symmetry or even non-PT. An exactly solvable model is presented to demonstrate the main points of this article.
http://arxiv.org/abs/1101.0351
Quantum Physics (quant-ph)
We investigate the connection between pseudo-Hermitian and Hermitian descriptions for a lattice, which consists of a set of isomorphic pseudo-Hermitian clusters. We show that such non-Hermitian systems can act as Hermitian systems. This is made possible by considering the dynamics of a state involving the superposition of a single eigenmode of each isomorphic clusters. It still holds when multiple eigenmodes are involved when additional restriction on the state is imposed. This Hermitian dynamics is demonstrated for the case of an exactly solvable PT-symmetric ladder system.