D. Krejcirik, P. Siegl, J. Zelezny
We consider one-dimensional Schroedinger-type operators in a bounded interval with non-self-adjoint Robin-type boundary conditions. It is well known that such operators are generically conjugate to normal operators via a similarity transformation. Motivated by recent interests in quasi-Hermitian Hamiltonians in quantum mechanics, we study properties of the transformations in detail. We show that they can be expressed as the sum of the identity and an integral Hilbert-Schmidt operator. In the case of parity and time reversal boundary conditions, we establish closed integral-type formulae for the similarity transformations, derive the similar self-adjoint operator and also find the associated “charge conjugation” operator, which plays the role of fundamental symmetry in a Krein-space reformulation of the problem.
http://arxiv.org/abs/1108.4946
Spectral Theory (math.SP); Mathematical Physics (math-ph); Functional Analysis (math.FA); Quantum Physics (quant-ph)
Myrta Grüning, Andrea Marini, Xavier Gonze
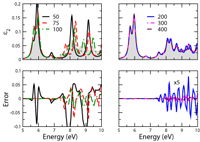The treatment of the Random-Phase Approximation Hamiltonians, encountered in different frameworks, like Time-Dependent Density Functional Theory or Bethe-Salpeter equation, is complicated by their non-Hermicity. Compared to their Hermitian Hamiltonian counterparts, computational methods for the treatment of non-Hermitian Hamiltonians are often less efficient and less stable, sometimes leading to the breakdown of the method. Recently [Gruning et al. Nano Lett. 8, 2820 (2009)], we have identified that such Hamiltonians are usually pseudo-Hermitian. Exploiting this property, we have implemented an algorithm of the Lanczos type for random-Phase Approximation Hamiltonians that benefits from the same stability and computational load as its Hermitian counterpart, and applied it to the study of the optical response of carbon nanotubes. We present here the related theoretical grounds and technical details, and study the performance of the algorithm for the calculation of the optical absorption of a molecule within the Bethe-Salpeter equation framework.
http://arxiv.org/abs/1102.3909
Materials Science (cond-mat.mtrl-sci); Mathematical Physics (math-ph)
Denis Borisov, David Krejcirik
The Laplacian in an unbounded tubular neighbourhood of a hyperplane with non-Hermitian complex-symmetric Robin-type boundary conditions is investigated in the limit when the width of the neighbourhood diminishes. We show that the Laplacian converges in a norm resolvent sense to a self-adjoint Schroedinger operator in the hyperplane whose potential is expressed solely in terms of the boundary coupling function. As a consequence, we are able to explain some peculiar spectral properties of the non-Hermitian Laplacian by known results for Schroedinger operators.
http://arxiv.org/abs/1102.5051
Spectral Theory (math.SP); Mathematical Physics (math-ph)
H. Hernandez-Coronado, D. Krejcirik, P. Siegl
![Transmissions |T|^2 as a function of energy k2 for the step-like potential <i>v</i> with a = Pi/4, epsilon_1 = 0.2, epsilon_3 = 0.5, beta_3 = -100, beta_2 = 0, beta_1 = -120 (continuous red line), and beta_1 = -200 (dashed blue line). See [5] for animated plots of |T|^2 as a function of potential.](http://ptsymmetry.net/wp-content/uploads/2010/11/figure4.png "figure4")
We establish that a perfect-transmission scattering problem can be described by a class of parity and time reversal symmetric operators and hereby we provide a scenario for understanding and implementing the corresponding quasi-Hermitian quantum mechanical framework from the physical viewpoint. One of the most interesting features of the analysis is that the complex eigenvalues of the underlying non-Hermitian problem, associated with a reflectionless scattering system, lead to the loss of perfect-transmission energies as the parameters characterizing the scattering potential are varied. On the other hand, the scattering data can serve to describe the spectrum of a large class of Schroedinger operators with complex Robin boundary conditions.
http://arxiv.org/abs/1011.4281
Mathematical Physics (math-ph); Quantum Physics (quant-ph)