Jean-Pierre Antoine, Camillo Trapani
A quasi-Hermitian operator is an operator that is similar to its adjoint in some sense, via a metric operator, i.e., a strictly positive self-adjoint operator. Whereas those metric operators are in general assumed to be bounded, we analyze the structure generated by unbounded metric operators in a Hilbert space. It turns out that such operators generate a canonical lattice of Hilbert spaces, that is, the simplest case of a partial inner product space (PIP-space). We introduce several generalizations of the notion of similarity between operators, in particular, the notion of quasi-similarity, and we explore to what extend they preserve spectral properties. Then we apply some of the previous results to operators on a particular PIP-space, namely, a scale of Hilbert spaces generated by a metric operator. Finally, motivated by the recent developments of pseudo-Hermitian quantum mechanics, we reformulate the notion of pseudo-Hermitian operators in the preceding formalism.
http://arxiv.org/abs/1409.3497
Mathematical Physics (math-ph)
Jean-Pierre Antoine, Camillo Trapani
A quasi-Hermitian operator is an operator that is similar to its adjoint in some sense, via a metric operator, i.e., a strictly positive self-adjoint operator. Whereas those metric operators are in general assumed to be bounded, we analyze the structure generated by unbounded metric operators in a Hilbert space. Following our previous work, we introduce several generalizations of the notion of similarity between operators. Then we explore systematically the various types of quasi-Hermitian operators, bounded or not. Finally we discuss their application in the so-called pseudo-Hermitian quantum mechanics.
http://arxiv.org/abs/1307.5644
Mathematical Physics (math-ph)
Myrta Grüning, Andrea Marini, Xavier Gonze
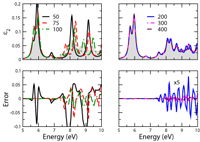The treatment of the Random-Phase Approximation Hamiltonians, encountered in different frameworks, like Time-Dependent Density Functional Theory or Bethe-Salpeter equation, is complicated by their non-Hermicity. Compared to their Hermitian Hamiltonian counterparts, computational methods for the treatment of non-Hermitian Hamiltonians are often less efficient and less stable, sometimes leading to the breakdown of the method. Recently [Gruning et al. Nano Lett. 8, 2820 (2009)], we have identified that such Hamiltonians are usually pseudo-Hermitian. Exploiting this property, we have implemented an algorithm of the Lanczos type for random-Phase Approximation Hamiltonians that benefits from the same stability and computational load as its Hermitian counterpart, and applied it to the study of the optical response of carbon nanotubes. We present here the related theoretical grounds and technical details, and study the performance of the algorithm for the calculation of the optical absorption of a molecule within the Bethe-Salpeter equation framework.
http://arxiv.org/abs/1102.3909
Materials Science (cond-mat.mtrl-sci); Mathematical Physics (math-ph)