Bijan Bagchi, Subhrajit Modak, Prasanta K. Panigrahi
The relevance of parity and time reversal (PT)-symmetric structures in optical systems is known for sometime with the correspondence existing between the Schrodinger equation and the paraxial equation of diffraction where the time parameter represents the propagating distance and the refractive index acts as the complex potential. In this paper, we systematically analyze a normalized form of the nonlinear Schrodinger system with two new families of PT-symmetric potentials in the presence of competing nonlinearities. We generate a class of localized eigenmodes and carry out a linear stability analysis on the solutions. In particular, we find an interesting feature of bifurcation charaterized by the parameter of perturbative growth rate passing through zero where a transition to imaginary eigenvalues occurs.
http://arxiv.org/abs/1307.7246
Quantum Physics (quant-ph); Mathematical Physics (math-ph); Exactly Solvable and Integrable Systems (nlin.SI)
B. Bagchi, A. Banerjee, A. Ganguly
This paper examines the features of a generalized position-dependent mass Hamiltonian in a supersymmetric framework in which the constraints of pseudo-Hermiticity and CPT are naturally embedded. Different representations of the charge operator are considered that lead to new mass-deformed superpotentials which are inherently PT-symmetric. The qualitative spectral behavior of the Hamiltonian is studied and several interesting consequences are noted.
http://arxiv.org/abs/1212.2122
Quantum Physics (quant-ph); High Energy Physics – Theory (hep-th); Mathematical Physics (math-ph)
B. Bagchi, A. Ghose Choudhury, Partha Guha
We explore the Jacobi Last Multiplier as a means for deriving the Lagrangian of a fourth-order differential equation. In particular we consider the classical problem of the Pais-Uhlenbeck oscillator and write down the accompanying Hamiltonian. We then compare such an expression with an alternative derivation of the Hamiltonian that makes use of the Ostrogradski’s method and show that a mapping from the one to the other is achievable by variable transformations. Assuming canonical quantization procedure to be valid we go for the operator version of the Hamiltonian that represents a pair of uncoupled oscillators. This motivates us to propose a generalized Pais-Uhlenbeck Hamiltonian in terms of the usual harmonic oscillator creation and annihilation operators by including terms quadratic and linear in them. Such a Hamiltonian turns out to be essentially non-Hermitian but has an equivalent Hermitian representation which is reducible to a typically position-dependent reduced mass form.
http://arxiv.org/abs/1212.2092
Mathematical Physics (math-ph); Quantum Physics (quant-ph)
Anjana Sinha
We apply the factorization technique developed by Kuru et. al. [Ann. Phys. {\bf 323} (2008) 413] to obtain the exact analytical classical trajectories and momenta of the continuum states of the non Hermitian but \(\cal{PT}\) symmetric Scarf II potential. In particular, we observe that the strange behaviour of the quantum version at the spectral singularity has an interesting classical analogue.
http://arxiv.org/abs/1206.6987
Quantum Physics (quant-ph); Mathematical Physics (math-ph)
Yogesh N. Joglekar, Bijan Bagchi
We investigate the effects of competition between two complex, \(\mathcal{PT}\)-symmetric potentials on the \(\mathcal{PT}\)-symmetric phase of a “particle in a box”. These potentials, given by \(V_Z(x)=iZ\mathrm{sign}(x)\) and \(V_\xi(x)=i\xi[\delta(x-a)-\delta(x+a)]\), represent long-range and localized gain/loss regions respectively. We obtain the \(\mathcal{PT}\)-symmetric phase in the \((Z,\xi)\) plane, and find that for locations \(\pm a\) near the edge of the box, the \(\mathcal{PT}\)-symmetric phase is strengthened by additional losses to the loss region. We also predict that a broken \(\mathcal{PT}\)-symmetry will be restored by increasing the strength \(\xi\) of the localized potential. By comparing the results for this problem and its lattice counterpart, we show that a robust \(\mathcal{PT}\)-symmetric phase in the continuum is consistent with the fragile phase on the lattice. Our results demonstrate that systems with multiple, \(\mathcal{PT}\)-symmetric potentials show unique, unexpected properties.
http://arxiv.org/abs/1206.3310
Quantum Physics (quant-ph)
Anjana Sinha
The study of a particle with position-dependent effective mass (pdem), within a double heterojunction is extended into the complex domain — when the region within the heterojunctions is described by a non Hermitian \({\cal{PT}}\) symmetric potential. After obtaining the exact analytical solutions, the reflection and transmission coefficients are calculated, and plotted as a function of the energy. It is observed that at least two of the characteristic features of non Hermitian \({\cal{PT}}\) symmetric systems — viz., left / right asymmetry and anomalous behaviour at spectral singularity, are preserved even in the presence of pdem. The possibility of charge conservation is also discussed.
http://arxiv.org/abs/1204.2416
Quantum Physics (quant-ph)
Andrea Cavaglia, Andreas Fring, Bijan Bagchi
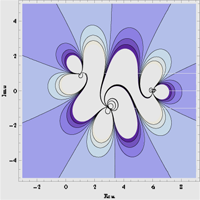We investigate complex versions of the Korteweg-deVries equations and an Ito type nonlinear system with two coupled nonlinear fields. We systematically construct rational, trigonometric/hyperbolic, elliptic and soliton solutions for these models and focus in particular on physically feasible systems, that is those with real energies. The reality of the energy is usually attributed to different realisations of an antilinear symmetry, as for instance PT-symmetry. It is shown that the symmetry can be spontaneously broken in two alternative ways either by specific choices of the domain or by manipulating the parameters in the solutions of the model, thus leading to complex energies. Surprisingly the reality of the energies can be regained in some cases by a further breaking of the symmetry on the level of the Hamiltonian. In many examples some of the fixed points in the complex solution for the field undergo a Hopf bifurcation in the PT-symmetry breaking process. By employing several different variants of the symmetries we propose many classes of new invariant extensions of these models and study their properties. The reduction of some of these models yields complex quantum mechanical models previously studied.
http://arxiv.org/abs/1103.1832
Mathematical Physics (math-ph); High Energy Physics – Theory (hep-th); Quantum Physics (quant-ph)
A. Sinha, D. Dutta, P. Roy
We apply the factorization technique developed by Kuru and Negro [Ann. Phys. 323 (2008) 413] to study complex classical systems. As an illustration we apply the technique to study the classical analogue of the exactly solvable PT symmetric Scarf II model, which exhibits the interesting phenomenon of spontaneous breakdown of PT symmetry at some critical point. As the parameters are tuned such that energy switches from real to complex conjugate pairs, the corresponding classical trajectories display a distinct characteristic feature – the closed orbits become open ones.
http://arxiv.org/abs/1101.0909
Quantum Physics (quant-ph)
Physics Letters A : vol. 375 (2011) p 452-457