H. F. Jones
Propagation of light through media with a complex refractive index in which gain and loss are engineered to be PT symmetric has many remarkable features. In particular the usual unitarity relations are not satisfied, so that the reflection coefficients can be greater than one, and in general are not the same for left or right incidence. Within the class of optical potentials of the form \(v(x)=v_1\cos(2\beta x)+iv_2\sin(2\beta x)\) the case \(v_2=v_1\) is of particular interest, as it lies on the boundary of PT-symmetry breaking. It has been shown in a recent paper by Lin et al. that in this case one has the property of “unidirectional invisibility”, while for propagation in the other direction there is a greatly enhanced reflection coefficient proportional to \(L^2\), where \(L\) is the length of the medium in the direction of propagation.
For this potential we show how analytic expressions can be obtained for the various transmission and reflection coefficients, which are expressed in a very succinct form in terms of modified Bessel functions. While our numerical results agree very well with those of Lin et al. we find that the invisibility is not quite exact, in amplitude or phase. As a test of our formulas we show that they identically satisfy a modified version of unitarity appropriate for PT-symmetric potentials. We also examine how the enhanced transmission comes about for a wave-packet, as opposed to a plane wave, finding that the enhancement now arises through an increase, of \(O(L)\), in the pulse length, rather than the amplitude.
http://arxiv.org/abs/1111.2041
Optics (physics.optics); Quantum Physics (quant-ph)
Gilles Demange, Eva-Maria Graefe
Parameter dependent non-Hermitian quantum systems typically not only possess eigenvalue degeneracies, but also degeneracies of the corresponding eigenfunctions at exceptional points. While the effect of two coalescing eigenfunctions on cyclic parameter variation is well investigated, little attention has hitherto been paid to the effect of more than two coalescing eigenfunctions. Here a characterisation of behaviours of symmetric Hamiltonians with three coalescing eigenfunctions is presented, using perturbation theory for non-Hermitian operators. Two main types of parameter perturbations need to be distinguished, which lead to characteristic eigenvalue and eigenvector patterns under cyclic variation. A physical system is introduced for which both behaviours might be experimentally accessible.
http://arxiv.org/abs/1110.1489
Quantum Physics (quant-ph); Mathematical Physics (math-ph)
Carl M. Bender, Hugh F. Jones
All of the PT-symmetric potentials that have been studied so far have been local. In this paper nonlocal PT-symmetric separable potentials of the form \(V(x,y)=i\epsilon[U(x)U(y)-U(-x)U(-y)]\), where \(U(x)\) is real, are examined. Two specific models are examined. In each case it is shown that there is a parametric region of the coupling strength $\epsilon$ for which the PT symmetry of the Hamiltonian is unbroken and the bound-state energies are real. The critical values of \(\epsilon\) that bound this region are calculated.
http://arxiv.org/abs/1107.2293
High Energy Physics – Theory (hep-th); Mathematical Physics (math-ph); Quantum Physics (quant-ph)
Dorje C. Brody, Eva-Maria Graefe
The dynamical aspects of a spin-1/2 particle in Hermitian coquaternionic quantum theory is investigated. It is shown that the time evolution exhibits three different characteristics, depending on the values of the parameters of the Hamiltonian. When energy eigenvalues are real, the evolution is either isomorphic to that of a complex Hermitian theory on a spherical state space, or else it remains unitary along an open orbit on a hyperbolic state space. When energy eigenvalues form a complex conjugate pair, the orbit of the time evolution closes again even though the state space is hyperbolic.
http://arxiv.org/abs/1105.4038
Mathematical Physics (math-ph); Quantum Physics (quant-ph)
Eva-Maria Graefe, H. F. Jones
The PT-symmetric potential \(V_0[\cos(2\pi x/a)+i\lambda\sin(2\pi x/a)]\) has a completely real spectrum for \(\lambda\le 1\), and begins to develop complex eigenvalues for \(\lambda>1\). At the symmetry-breaking threshold \(\lambda=1\) some of the eigenvectors become degenerate, giving rise to a Jordan-block structure for each degenerate eigenvector. In general this is expected to result in a secular growth in the amplitude of the wave. However, it has been shown in a recent paper by Longhi, by numerical simulation and by the use of perturbation theory, that for a broad initial wave packet this growth is suppressed, and instead a saturation leading to a constant maximum amplitude is observed. We revisit this problem by explicitly constructing the Bloch wave-functions and the associated Jordan functions and using the method of stationary states to find the dependence on the longitudinal distance \(z\) for a variety of different initial wave packets. This allows us to show in detail how the saturation of the linear growth arises from the close connection between the contributions of the Jordan functions and those of the neighbouring Bloch waves.
http://arxiv.org/abs/1104.2838
Optics (physics.optics); Quantum Physics (quant-ph)
Dorje C Brody, Eva-Maria Graefe
While real Hamiltonian mechanics and Hermitian quantum mechanics can both be cast in the framework of complex canonical equations, their complex generalisations have hitherto been remained tangential. In this paper quaternionic and coquaternionic (split-signature analogue of quaternions) extensions of Hamiltonian mechanics are introduced, and are shown to offer a unifying framework for complexified classical and quantum mechanics. In particular, quantum theories characterised by complex Hamiltonians invariant under space-time reflection are shown to be equivalent to certain coquaternionic extensions of Hermitian quantum theories. One of the interesting consequences is that the space-time dimension of these systems is six, not four, on account of the structures of coquaternionic quantum mechanics.
http://arxiv.org/abs/1012.0757
Mathematical Physics (math-ph); High Energy Physics – Theory (hep-th); Quantum Physics (quant-ph)
Carl M. Bender, Dorje C. Brody, Joao Caldeira, Bernard K. Meister
Suppose that a system is known to be in one of two quantum states, $|\psi_1 > $ or $|\psi_2 >$. If these states are not orthogonal, then in conventional quantum mechanics it is impossible with one measurement to determine with certainty which state the system is in. However, because a non-Hermitian PT-symmetric Hamiltonian determines the inner product that is appropriate for the Hilbert space of physical states, it is always possible to choose this inner product so that the two states $|\psi_1 > $ and $|\psi_2 > $ are orthogonal. Thus, quantum state discrimination can, in principle, be achieved with a single measurement.
http://arxiv.org/abs/1011.1871
High Energy Physics – Theory (hep-th); Mathematical Physics (math-ph); Quantum Physics (quant-ph)
Carl M. Bender, Daniel W. Hook
Classical mechanics is a singular theory in that real-energy classical particles can never enter classically forbidden regions. However, if one regulates classical mechanics by allowing the energy E of a particle to be complex, the particle exhibits quantum-like behavior: Complex-energy classical particles can travel between classically allowed regions separated by potential barriers. When Im(E) -> 0, the classical tunneling probabilities persist. Hence, one can interpret quantum tunneling as an anomaly. A numerical comparison of complex classical tunneling probabilities with quantum tunneling probabilities leads to the conjecture that as ReE increases, complex classical tunneling probabilities approach the corresponding quantum probabilities. Thus, this work attempts to generalize the Bohr correspondence principle from classically allowed to classically forbidden regions.
http://arxiv.org/abs/1011.0121
High Energy Physics – Theory (hep-th); Mathematical Physics (math-ph); Quantum Physics (quant-ph)
Eva-Maria Graefe, Roman Schubert
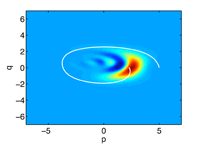The quantum evolution of the Wigner function for Gaussian wave packets generated by a non-Hermitian Hamiltonian is investigated. In the semiclassical limit $\hbar\to 0$ this yields the non-Hermitian analog of the Ehrenfest theorem for the dynamics of observable expectation values. The lack of Hermiticity reveals the importance of the complex structure on the classical phase space: The resulting equations of motion are coupled to an equation of motion for the phase space metric—a phenomenon having no analogue in Hermitian theories. Furthermore, example studies show that the anti-Hermitian term can improve the accuracy of the classical approximation.
http://arxiv.org/abs/1010.4557
Quantum Physics (quant-ph); Mathematical Physics (math-ph)
H. F. Jones
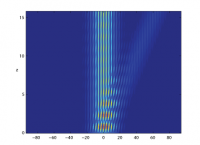We show how the band structure and beam dynamics of non-Hermitian $PT$-symmetric sinusoidal optical lattices can be approached from the point of view of the equivalent Hermitian problem, obtained by an analytic continuation in the transverse spatial variable $x$. In this latter problem the eigenvalue equation reduces to the Mathieu equation, whose eigenfunctions and properties have been well studied. That being the case, the beam propagation, which parallels the time-development of the wave-function in quantum mechanics, can be calculated using the equivalent of the method of stationary states. We also discuss a model potential that interpolates between a sinusoidal and periodic square well potential, showing that some of the striking properties of the sinusoidal potential, in particular birefringence, become much less prominent as one goes away from the sinusoidal case.
http://arxiv.org/abs/1009.5784
Optics (physics.optics); Quantum Physics (quant-ph)
