Eva-Maria Graefe, H. F. Jones
The PT-symmetric potential \(V_0[\cos(2\pi x/a)+i\lambda\sin(2\pi x/a)]\) has a completely real spectrum for \(\lambda\le 1\), and begins to develop complex eigenvalues for \(\lambda>1\). At the symmetry-breaking threshold \(\lambda=1\) some of the eigenvectors become degenerate, giving rise to a Jordan-block structure for each degenerate eigenvector. In general this is expected to result in a secular growth in the amplitude of the wave. However, it has been shown in a recent paper by Longhi, by numerical simulation and by the use of perturbation theory, that for a broad initial wave packet this growth is suppressed, and instead a saturation leading to a constant maximum amplitude is observed. We revisit this problem by explicitly constructing the Bloch wave-functions and the associated Jordan functions and using the method of stationary states to find the dependence on the longitudinal distance \(z\) for a variety of different initial wave packets. This allows us to show in detail how the saturation of the linear growth arises from the close connection between the contributions of the Jordan functions and those of the neighbouring Bloch waves.
http://arxiv.org/abs/1104.2838
Optics (physics.optics); Quantum Physics (quant-ph)
Derek D. Scott, Yogesh N. Joglekar
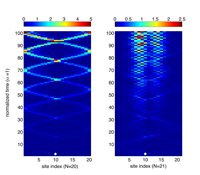We investigate the robustness of parity- and time-reversal PT-symmetric phase in an N-site lattice with position-dependent, parity-symmetric hopping function and a pair of imaginary, PT-symmetric impurities. We find that the “fragile” PT-symmetric phase in these lattices is stronger than its counterpart in a lattice with constant hopping. With an open system in mind, we explore the degrees of broken PT symmetry and their signatures in single-particle wavepacket evolution. We predict that when the PT-symmetric impurities are closest to each other, the time evolution of a wavepacket in an even-N lattice is remarkably different from that in an odd-$N$ lattice. Our results suggest that PT-symmetry breaking in such lattices is accompanied by rich, hitherto unanticipated, phenomena.
http://arxiv.org/abs/1104.1666
Quantum Physics (quant-ph); Quantum Gases (cond-mat.quant-gas)
Andrey E. Miroshnichenko, Boris A. Malomed, Yuri S. Kivshar
We introduce a class of PT-symmetric systems which include mutually matched nonlinear loss and gain (inother words, a class of PT-invariant Hamiltonians in which both the harmonic and anharmonic parts are non-Hermitian). For a basic system in the form of a dimer, symmetric and asymmetric eigenstates, including multistable ones, are found analytically. We demonstrate that, if coupled to a linear chain, such a nonlinear PT-symmetric dimer generates new types of nonlinear resonances, with the completely suppressed or greatly amplified transmission, as well as a regime similar to the electromagnetically-induced transparency (EIT). The implementation of the systems is possible in various media admitting controllable linear and nonlinear amplification of waves.
http://arxiv.org/abs/1104.0849
Mathematical Physics (math-ph)
Per Alexandersson
In this paper, we generalize several results of the article “Analytic continuation of eigenvalues of a quartic oscillator” of A. Eremenko and A. Gabrielov. We consider a family of eigenvalue problems for a Schr\”odinger equation with even polynomial potentials of arbitrary degree d with complex coefficients, and k<(d+2)/2 boundary conditions. We show that the spectral determinant in this case consists of two components, containing even and odd eigenvalues respectively.
In the case with k=(d+2)/2 boundary conditions, we show that the corresponding parameter space consists of infinitely many connected components.
http://arxiv.org/abs/1104.0593v1
Mathematical Physics (math-ph)
Alexander Szameit, Mikael C. Rechtsman, Omri Bahat-Treidel, Mordechai Segev
We apply gain/loss to honeycomb photonic lattices and demonstrate that optical tachyons, a photonic version of particles that travel faster than the speed of light, can be generated by PT-symmetry breaking in this structure. We further show that the PT-symmetry can be restored via strain.
http://arxiv.org/abs/1103.3389
Optics (physics.optics)
Miloslav Znojil
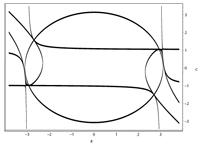The “Hermitizability” problem of quantum theory is explained, discussed and illustrated via the discrete-lattice cryptohermitian quantum graphs. In detail, the description of the domain ${\cal D}$ of admissible parameters is provided for the “circular-model” three-parametric quantum Hamiltonian $H$ using periodic boundary conditions. It is emphasized that even in such an elementary system the weak- and strong-coupling subdomains of ${\cal D}$ become, unexpectedly, non-empty and disconnected.
http://arxiv.org/abs/1103.4001
Quantum Physics (quant-ph); High Energy Physics – Theory (hep-th); Mathematical Physics (math-ph)
Alexander Szameit, Mikael C. Rechtsman, Omri Bahat-Treidel, Mordechai Segev
We apply gain/loss to honeycomb photonic lattices and show that the dispersion relation is identical to tachyons – particles with imaginary mass that travel faster than the speed of light. This is accompanied by PT-symmetry breaking in this structure. We further show that the PT-symmetry can be restored by deforming the lattice.
http://arxiv.org/abs/1103.3389
Optics (physics.optics)
Luis B. Castro
The relativistic problem of fermions subject to a PT-symmetric potential in the presence of position-dependent mass is reinvestigated. The influence of the PT-symmetric potential in the continuity equation and in the orthonormalization condition are analyzed. In addition, a misconception diffused in the literature on the interaction of neutral fermions is clarified.
http://arxiv.org/abs/1103.2460
Quantum Physics (quant-ph); High Energy Physics – Theory (hep-th); Mathematical Physics (math-ph)
Andrea Cavaglia, Andreas Fring, Bijan Bagchi
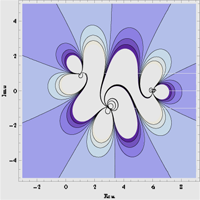We investigate complex versions of the Korteweg-deVries equations and an Ito type nonlinear system with two coupled nonlinear fields. We systematically construct rational, trigonometric/hyperbolic, elliptic and soliton solutions for these models and focus in particular on physically feasible systems, that is those with real energies. The reality of the energy is usually attributed to different realisations of an antilinear symmetry, as for instance PT-symmetry. It is shown that the symmetry can be spontaneously broken in two alternative ways either by specific choices of the domain or by manipulating the parameters in the solutions of the model, thus leading to complex energies. Surprisingly the reality of the energies can be regained in some cases by a further breaking of the symmetry on the level of the Hamiltonian. In many examples some of the fixed points in the complex solution for the field undergo a Hopf bifurcation in the PT-symmetry breaking process. By employing several different variants of the symmetries we propose many classes of new invariant extensions of these models and study their properties. The reduction of some of these models yields complex quantum mechanical models previously studied.
http://arxiv.org/abs/1103.1832
Mathematical Physics (math-ph); High Energy Physics – Theory (hep-th); Quantum Physics (quant-ph)
Harald Fritzsch, Zhi-zhong Xing, Ye-Ling Zhou
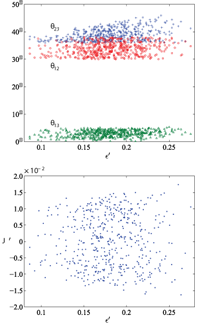We show that non-Hermitian and nearest-neighbor-interacting perturbations to the Fritzsch textures of lepton and quark mass matrices can make both of them fit current experimental data very well. In particular, we obtain \theta_{23} \simeq 45^\circ for the atmospheric neutrino mixing angle and predict \theta_{13} \simeq 3^\circ to 6^\circ for the smallest neutrino mixing angle when the perturbations in the lepton sector are at the 20% level. The same level of perturbations is required in the quark sector, where the Jarlskog invariant of CP violation is about 3.7 \times 10^{-5}. In comparison, the strength of leptonic CP violation is possible to reach about 1.5 \times 10^{-2} in neutrino oscillations.
http://arxiv.org/abs/1101.4272
High Energy Physics – Phenomenology (hep-ph)