Andreas Fring, Monique Smith
We provide a general construction procedure for antilinearly invariant complex root spaces. The proposed method is generic and may be applied to any Weyl group allowing to take any element of the group as a starting point for the construction. Worked out examples for several specific Weyl groups are presented, focusing especially on those cases for which no solutions were found previously. When applied in the defining relations of models based on root systems this usually leads to non-Hermitian models, which are nonetheless physically viable in a self-consistent sense as they are antilinearly invariant by construction. We discuss new types of Calogero models based on these complex roots. In addition we propose an alternative construction leading to q-deformed roots. We employ the latter type of roots to formulate a new version of affine Toda field theories based on non-simply laced roots systems. These models exhibit on the classical level a strong-weak duality in the coupling constant equivalent to a Lie algebraic duality, which is known for the quantum version of the undeformed case.
http://arxiv.org/abs/1108.1719
High Energy Physics – Theory (hep-th); Mathematical Physics (math-ph); Quantum Physics (quant-ph)
Miloslav Znojil
Non-Hermitian ring-shaped discrete lattices share the appeal with their more popular linear predecessors. Their dynamics controlled by the nearest-neighbor interaction is equally phenomenologically interesting. In comparison, the innovative nontriviality of their topology may be expected to lead to new spectral effects. Some of them are studied here via solvable examples. Main attention is paid to the perturbation-caused removals of spectral degeneracy at exceptional points.
http://arxiv.org/abs/1108.0620
Quantum Physics (quant-ph); Mathematical Physics (math-ph)
A.V. Sokolov
This part is a continuation of the Part I where we built resolutions of identity for certain non-Hermitian Hamiltonians constructed from biorthogonal sets of their eigen- and associated functions for the spectral problem defined on entire axis. Non-Hermitian Hamiltonians under consideration were taken with continuous spectrum and the following cases were examined: an exceptional point situated on a boundary of continuous spectrum and an exceptional point situated inside of continuous spectrum. In the present work the rigorous proofs are given for the resolutions of identity in both cases.
http://arxiv.org/abs/1107.5916
Mathematical Physics (math-ph); High Energy Physics – Theory (hep-th); Nuclear Theory (nucl-th); Quantum Physics (quant-ph)
A.A. Andrianov, A.V. Sokolov
Resolutions of identity for certain non-Hermitian Hamiltonians constructed from biorthogonal sets of their eigen- and associated functions are given for the spectral problem defined on entire axis. Non-Hermitian Hamiltonians under consideration are taken with continuous spectrum and the following peculiarities are investigated: (1) the case when there is an exceptional point situated on a boundary of continuous spectrum; (2) the case when there is an exceptional point situated inside of continuous spectrum. The reductions of the derived resolutions of identity under narrowing of the classes of employed test functions are revealed. It is shown that in the case (1) some of associated functions included into the resolution of identity are normalizable and some of them may be not and in the case (2) the bounded associated function corresponding to the exceptional point does not belong to the physical state space. Spectral properties of a SUSY partner Hamiltonian for the Hamiltonian with an exceptional point are examined.
http://arxiv.org/abs/1107.5911
Mathematical Physics (math-ph); High Energy Physics – Theory (hep-th); Nuclear Theory (nucl-th); Quantum Physics (quant-ph)
Sergii Kuzhel, Oleksii Patsiuk
Let \(J\) and \(R\) be anti-commuting fundamental symmetries in a Hilbert space \(\mathfrak{H}\). The operators \(J\) and \(R\) can be interpreted as basis (generating) elements of the complex Clifford algebra \({\mathcal C}l_2(J,R):={span}\{I, J, R, iJR\}\). An arbitrary non-trivial fundamental symmetry from \({\mathcal C}l_2(J,R)\) is determined by the formula \(J_{\vec{\alpha}}=\alpha_{1}J+\alpha_{2}R+\alpha_{3}iJR\), where \({\vec{\alpha}}\in\mathbb{S}^2\). Let \(S\) be a symmetric operator that commutes with \({\mathcal C}l_2(J,R)\). The purpose of this paper is to study the sets \(\Sigma_{{J_{\vec{\alpha}}}}\) (\(\forall{\vec{\alpha}}\in\mathbb{S}^2)\) of self-adjoint extensions of \(S\) in Krein spaces generated by fundamental symmetries \({{J_{\vec{\alpha}}}}\) (\({{J_{\vec{\alpha}}}}\)-self-adjoint extensions). We show that the sets \(\Sigma_{{J_{\vec{\alpha}}}}\) and \(\Sigma_{{J_{\vec{\beta}}}}\) are unitarily equivalent for different \({\vec{\alpha}}, {\vec{\beta}}\in\mathbb{S}^2\) and describe in detail the structure of operators \(A\in\Sigma_{{J_{\vec{\alpha}}}}\) with empty resolvent set.
http://arxiv.org/abs/1105.2969
Functional Analysis (math.FA); Mathematical Physics (math-ph)
Jun-Qing Li, Yan-Gang Miao, Zhao Xue
An algebraic method for pseudo-hermitian systems is proposed through redefining annihilation and creation operators which are pseudo-hermitian adjoint to each other. As an example, a parity-pseudo-hermitian Hamiltonian is constructed and then analyzed in detail. Its real spectrum is obtained by means of the algebraic method, in which a new operator $V$ is introduced in order to define new annihilation and creation operators and to keep pseudo-hermitian inner products positive definite. It is shown that this P-pseudo-hermitian Hamiltonian also possesses PV-pseudo-hermiticity, where PV ensures a positive definite inner product. Moreover, when the parity-pseudo-hermitian system is extended to the canonical noncommutative space with noncommutative spatial coordinates and noncommutative momenta as well, the first order noncommutative correction of energy levels is calculated, and in particular the reality of energy spectra and the positive definiteness of inner products are found to be not altered by the noncommutativity.
http://arxiv.org/abs/1107.4972
Quantum Physics (quant-ph); High Energy Physics – Theory (hep-th)
S. Bittner, B. Dietz, U. Guenther, H. L. Harney, M. Miski-Oglu, A. Richter, F. Schaefer
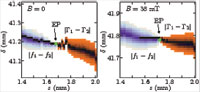We demonstrate the presence of parity-time (PT) symmetry for the non-Hermitian two-state Hamiltonian of a dissipative microwave billiard in the vicinity of an exceptional point (EP). The shape of the billiard depends on two parameters. The Hamiltonian is determined from the measured resonance spectrum on a fine grid in the parameter plane. On a curve, which passes through the EP, the Hamiltonian has either real or complex conjugate eigenvalues. An appropriate basis choice reveals its PT symmetry. Spontaneous symmetry breaking occurs at the EP.
http://arxiv.org/abs/1107.4256
Quantum Physics (quant-ph); Mathematical Physics (math-ph)
L. Jin, Z. Song
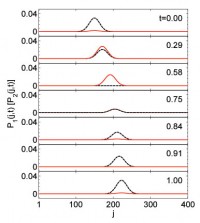We investigate the connection between pseudo-Hermitian and Hermitian descriptions for a lattice, which consists of a set of isomorphic pseudo-Hermitian clusters. We show that such non-Hermitian systems can act as Hermitian systems. This is made possible by considering the dynamics of a state involving the superposition of a single eigenmode of each isomorphic clusters. It still holds when multiple eigenmodes are involved when additional restriction on the state is imposed. This Hermitian dynamics is demonstrated for the case of an exactly solvable PT-symmetric ladder system.
http://arxiv.org/abs/1107.4311
Quantum Physics (quant-ph)
Carl M. Bender, Hugh F. Jones
All of the PT-symmetric potentials that have been studied so far have been local. In this paper nonlocal PT-symmetric separable potentials of the form \(V(x,y)=i\epsilon[U(x)U(y)-U(-x)U(-y)]\), where \(U(x)\) is real, are examined. Two specific models are examined. In each case it is shown that there is a parametric region of the coupling strength $\epsilon$ for which the PT symmetry of the Hamiltonian is unbroken and the bound-state energies are real. The critical values of \(\epsilon\) that bound this region are calculated.
http://arxiv.org/abs/1107.2293
High Energy Physics – Theory (hep-th); Mathematical Physics (math-ph); Quantum Physics (quant-ph)
Ali Mostafazadeh, Mustafa Sarisaman
The mathematical notion of a spectral singularity admits a physical interpretation as a zero-width resonance. It finds an optical realization as a certain type of lasing effect that occurs at the threshold gain. We explore spectral singularities of a complex spherical barrier potential and study their realization as transverse spherical electromagnetic waves emitted by a gain medium with a spherical geometry. In particular, for a typical dye laser material, we obtain a lower bound on the size of the gain medium for the occurence of this kind of spectral singularities.
http://arxiv.org/abs/1107.1873
Mathematical Physics (math-ph); Optics (physics.optics); Quantum Physics (quant-ph)
